
 如圖,已知△ABC內(nèi)接于⊙O,AB是直徑,OD⊥BC于點(diǎn)D.連接DO并延長到F使AF=OC.
如圖,已知△ABC內(nèi)接于⊙O,AB是直徑,OD⊥BC于點(diǎn)D.連接DO并延長到F使AF=OC.分析 (1)證出△AOF和△AOC是等邊三角形,由SAS即可證出;△AOC≌△OAF;
(2)要四邊形OCAF是菱形,需OC=CA=AF=OF,即△AOC為等腰三角形,∠2=60°,那么∠1=30°.
解答 (1)證明:∵AF=OC=OF=AO,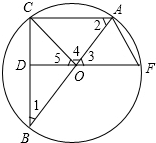
∴△AOF為等邊三角形,
∴∠3=60°,且∠3=∠DOB=60°,
又∵OD⊥BC,
∴D是BC的中點(diǎn),∠1=30°;
∵AB是直徑,
∴∠ACB=90°,
∴∠2=60°,
∴△AOC是等邊三角形,
∵△AOF是等邊三角形,
∴AF=OC=OF=AO,
在△AOC和△OAF中,$\left\{\begin{array}{l}{AC=OF}&{\;}\\{∠2=∠3}&{\;}\\{OA=AO}&{\;}\end{array}\right.$,
∴△AOC≌△AOF(SAS);
(2)解:當(dāng)∠1=30°時(shí),四邊形OCAF是菱形.理由如下:
∵∠1=30°AB是直徑,
∴∠BCA=90°,
∴∠2=60°,而OC=OA,
∴△OAC是等邊三角形,
∴OA=OC=CA,
又∵D,O分別是BC,BA的中點(diǎn),
∴DO∥CA,
∴∠2=∠3=60°而OC=OA=AF.
∴△OAF是等邊三角形,
∴AF=OA=OF,(9分)
∴OC=CA=AF=OF,
∴四邊形OCAF是菱形.
點(diǎn)評(píng) 本題考查了全等三角形的判定、等邊三角形的判定與性質(zhì)、菱形的判定、圓周角定理、三角形中位線定理;熟練掌握全等三角形的判定和菱形的判定,證明三角形是等邊三角形是解決問題的關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知不等式組$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$,
已知不等式組$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$,查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
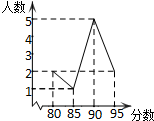 某班10名學(xué)生成績統(tǒng)計(jì)如圖,則這10名學(xué)生成績中位數(shù)是90分,眾數(shù)是90分.
某班10名學(xué)生成績統(tǒng)計(jì)如圖,則這10名學(xué)生成績中位數(shù)是90分,眾數(shù)是90分.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 要從甲、乙兩名同學(xué)中選出一名,代表班級(jí)參加射擊比賽,如圖是兩人最近10次射擊訓(xùn)練成績的折線統(tǒng)計(jì)圖.(兩同學(xué)的射擊成績都取整數(shù)環(huán))
要從甲、乙兩名同學(xué)中選出一名,代表班級(jí)參加射擊比賽,如圖是兩人最近10次射擊訓(xùn)練成績的折線統(tǒng)計(jì)圖.(兩同學(xué)的射擊成績都取整數(shù)環(huán))查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,把兩個(gè)大小相同的含30°的角的三角尺如圖放置,若AD=4$\sqrt{6}$,試求圍成的△ADC的面積.
如圖,把兩個(gè)大小相同的含30°的角的三角尺如圖放置,若AD=4$\sqrt{6}$,試求圍成的△ADC的面積.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com