
【題目】如圖,已知正方形OABC的邊OA在y軸的正半軸上,OC在x軸的正半軸上,OA=AB=2,拋物線y=![]() x2+bx+c經過點A,B,交正x軸于點D,E是OC上的動點(不與C重合)連接EB,過B點作BF⊥BE交y軸與F
x2+bx+c經過點A,B,交正x軸于點D,E是OC上的動點(不與C重合)連接EB,過B點作BF⊥BE交y軸與F
(1)求b,c的值及D點的坐標;
(2)求點E在OC上運動時,四邊形OEBF的面積有怎樣的規律性?并證明你的結論;
(3)連接EF,BD,設OE=m,△BEF與△BED的面積之差為S,問:當m為何值時S最小,并求出這個最小值.

【答案】(1)b=![]() ,c=2;D點坐標為(3,0).(2)點E在OC上運動時,四邊形OEBF的面積不變;(3)當m=2﹣
,c=2;D點坐標為(3,0).(2)點E在OC上運動時,四邊形OEBF的面積不變;(3)當m=2﹣![]() 時S最小為0.
時S最小為0.
【解析】
試題分析:(1)把點A,B代入拋物線y=![]() x2+bx+c求得b、c即可,y=0,建立方程求得點D;
x2+bx+c求得b、c即可,y=0,建立方程求得點D;
(2)四邊形OEBF的面積不變,利用三角形全等證得結論即可;
(3)用m分別表示出兩個三角形的面積,求差探討得出答案即可.
試題解析:(1)把點A(0,2)、B(2,2)代入拋物線y=![]() x2+bx+c得
x2+bx+c得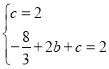
解得b=![]() ,c=2;
,c=2;
∴y=![]() x2+
x2+![]() x+2;
x+2;
令![]() x2+
x2+![]() x+2=0
x+2=0
解得x1=﹣1,x2=3
∴D點坐標為(3,0).
(2)點E在OC上運動時,四邊形OEBF的面積不變;
∵四邊形OABC是正方形
∴AB=BC,∠BCE=∠BAE=∠ABC=90°
又∵BF⊥BE
∴∠FBE=90°
∴∠ABF=∠CBE
∴△ABF≌△BCE
∴四邊形OEBF的面積始終等于正方形OABC的面積.
(3)如圖,
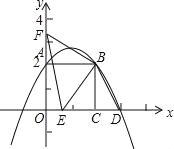
可以看出S△BEF=S梯形OCBF﹣S△OEF﹣S△BEC
=![]() (2+2+m)×2﹣
(2+2+m)×2﹣![]() m(2+m)﹣
m(2+m)﹣![]() (2﹣m)×2
(2﹣m)×2
=﹣![]() m2+m+2
m2+m+2
S△BED=![]() ×(3﹣m)×2
×(3﹣m)×2
=3﹣m
兩個三角形的面積差最小為0,
即3﹣m=﹣![]() m2+m+,
m2+m+,
解得m=2±![]() ,
,
∵E是OC上的動點
∴m=2﹣![]() ,
,
當m=2﹣![]() 時S最小為0.
時S最小為0.


科目:初中數學 來源: 題型:
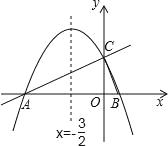
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣
x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣![]() 且經過A、C兩點,與x軸的另一交點為點B.
且經過A、C兩點,與x軸的另一交點為點B.
(1)①直接寫出點B的坐標;②求拋物線解析式.
(2)若點P為直線AC上方的拋物線上的一點,連接PA,PC.求△PAC的面積的最大值,并求出此時點P的坐標.
(3)拋物線上是否存在點M,過點M作MN垂直x軸于點N,使得以點A、M、N為頂點的三角形與△ABC相似?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】由上饒到南昌的某一次列車,運行途中停靠的車站依次是:上饒﹣橫峰﹣弋陽﹣貴溪﹣鷹潭﹣余江﹣東鄉﹣蓮塘﹣南昌,那么要為這次列車制作的火車票有( )
A.9種
B.18種
C.36種
D.72種
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設邊長為4的正方形的對角線長為x.
(1)x是有理數嗎?說說你的理由;
請你估計一下x在哪兩個相鄰整數之間?
估計x的值(結果精確到十分位);
如果結果精確到百分位呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家統計局的統計數據顯示:2013年全國糧食總產量達到6.0193億噸,比上年增長2.1%,6.0193億噸用科學記數法表示為( )
A. 61.093×107噸B. 6.1093×107噸C. 0.61093×109 噸D. 6.1093×108噸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com