
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑作半圓
為直徑作半圓![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)如果![]() 的徑為5,
的徑為5,![]() ,求
,求![]() 的長.
的長.
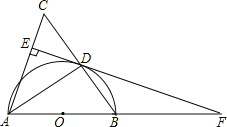
【答案】(1)見解析;(2)![]()
【解析】
(1)連接OD,AB為⊙O的直徑得∠ADB=90°,由AB=AC,根據等腰三角形性質得AD平分BC,即DB=DC,則OD為△ABC的中位線,所以OD∥AC,而DE⊥AC,則OD⊥DE,然后根據切線的判定方法即可得到結論.
(2)由∠DAC=∠DAB,根據等角的余角相等得∠ADE=∠ABD,在Rt△ADB中,利用解直角三角形的方法可計算出AD=8,在Rt△ADE中可計算出AE的長.
解:(1)證明:連結OD,如圖,
∵AB為⊙0的直徑,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD為△ABC的中位線,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴EF是⊙O的切線;
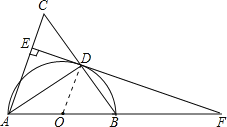
(2)∵△ABC是等腰三角形,
∴∠CAD=∠BAD,
∵∠AED=∠ADB=90°,
∴∠CAD+∠ADE=∠BAD+∠ABD=90°,
∴∠ADE=∠ABD,
在Rt△ABD中,sin∠ABD=sin∠ADE=![]() ,
,
AB=2AO=10,
∴AD=8,
在Rt△ADE中,sin∠ADE=![]() ,
,
∴AE=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
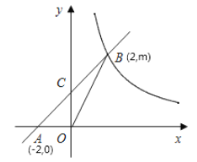
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與反比例函數第一象限內的圖象交于點
,與反比例函數第一象限內的圖象交于點![]() ,連接
,連接![]() ,若
,若![]() .
.
(1)求直線![]() 的表達式和反比例函數的表達式;
的表達式和反比例函數的表達式;
(2)若直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸相交于點C(0,﹣4).
的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸相交于點C(0,﹣4).
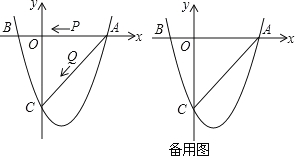
(1)求該二次函數的解析;
(2)若點P、Q同時從A點出發,以每秒1個單位長度的速度分別沿AB、AC邊運動,其中一點到達端點時,另一點也隨之停止運動.
①當點P運動到B點時,在x軸上是否存在點E,使得以A、E、Q為頂點的三角形為等腰三角形?若存在,請求出E點的坐標;若不存在,請說明理由.
②當P、Q運動到t秒時,△APQ沿PQ翻折,點A恰好落在拋物線上D點處,請直接寫出t的值及D點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
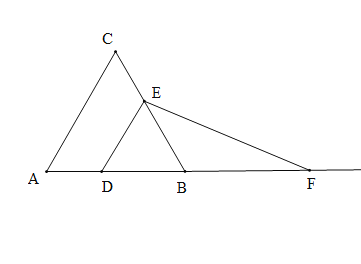
【題目】如圖,已知![]() 為等邊三角形,
為等邊三角形,![]() ,點
,點![]() 為邊
為邊![]() 上一點,過點
上一點,過點![]() 作
作![]() .交
.交![]() 于
于![]() 點;過
點;過![]() 點作
點作![]() ,交
,交![]() 的延長線于
的延長線于![]() 點.設
點.設![]() ,
,![]() 的面積為
的面積為![]() ,則能大致反映
,則能大致反映![]() 與
與![]() 函數關系的圖象是( )
函數關系的圖象是( )
A.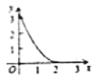 B.
B.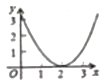
C.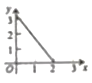 D.
D.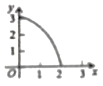
查看答案和解析>>
科目:初中數學 來源: 題型:
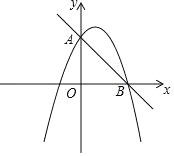
【題目】如圖,直線y=﹣x+4與拋物線y=﹣![]() x2+bx+c交于A,B兩點,點A在y軸上,點B在x軸上.
x2+bx+c交于A,B兩點,點A在y軸上,點B在x軸上.
(1)求拋物線的解析式;
(2)在x軸下方的拋物線上存在一點P,使得∠ABP=90°,求出點P坐標;
(3)點E是拋物線對稱軸上一點,點F是拋物線上一點,是否存在點E和點F使得以點E,F,B,O為頂點的四邊形是平行四邊形?若存在,求出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=kx+2k(k>0)與x軸交于點P,與雙曲線![]() (x>0)交于點Q,若直線y=4kx-2與直線PQ交于點R(點R在點Q右側),當RQ≤PQ時,k的取值范圍是__.
(x>0)交于點Q,若直線y=4kx-2與直線PQ交于點R(點R在點Q右側),當RQ≤PQ時,k的取值范圍是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
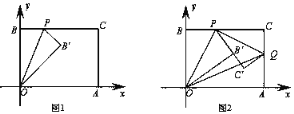
【題目】已知一個矩形紙片OACB,將該紙片放置在平面直角坐標系中,點A(4,0),點B(0,3),點P為BC邊上的動點(點P不與點B、C重合),經過點O、P折疊該紙片,得點B′和折痕OP.設BP=t.
(1)如圖1,當∠BOP=30°時,求點P的坐標;
(2)如圖2,經過點P再次折疊紙片,使點C落在直線PB′上,得點C′和折痕PQ,設AQ=m,試用含有t的式子表示m;
(3)在(2)的條件下,連接OQ,當OQ取得最小值時,求點Q的坐標;
(4)在(2)的條件下,點C′能否落在邊OA上?如果能,直接寫出點P的坐標;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年疫情期間,為了更好地落實“停課不停學”行動,我市某中學為了更好督促學生學習,組織教師對某班學生進行家訪,根據學生參加網絡學習效果劃分為![]() (差),
(差),![]() (中),
(中),![]() (優),
(優),![]() (良)四個等級,并繪制了下面不完整的統計圖表,根據圖表中提供的信息解答下列問題;
(良)四個等級,并繪制了下面不完整的統計圖表,根據圖表中提供的信息解答下列問題;
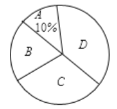
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 等級對應扇形圓心角的度數;
等級對應扇形圓心角的度數;
(3)學校要從![]() 等級的學生中隨機選取2人參加李老師個性化輔導,用列表或畫樹狀圖求
等級的學生中隨機選取2人參加李老師個性化輔導,用列表或畫樹狀圖求![]() 等級中的學生小慧被選中參加輔導的概率.
等級中的學生小慧被選中參加輔導的概率.
效果等級 | 頻數 | 頻率 |
| 5 | |
| ||
|
| 0.3 |
| 20 |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是![]() 的直徑,點P在BA的延長線上,PD切
的直徑,點P在BA的延長線上,PD切![]() 于點D,過點B作
于點D,過點B作![]() ,交PD的延長線于點C,連接AD并延長,交BE于點E.
,交PD的延長線于點C,連接AD并延長,交BE于點E.
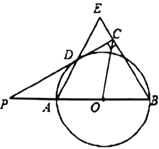
(Ⅰ)求證:AB=BE;
(Ⅱ)連結OC,如果PD=2![]() ,∠ABC=60°,求OC的長.
,∠ABC=60°,求OC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com