
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2![]() ,點(diǎn)P為AB邊上的一個(gè)動(dòng)點(diǎn),連接PC,過點(diǎn)P作PQ⊥PC交BC邊于點(diǎn)Q,則BQ的最大值為_____.
,點(diǎn)P為AB邊上的一個(gè)動(dòng)點(diǎn),連接PC,過點(diǎn)P作PQ⊥PC交BC邊于點(diǎn)Q,則BQ的最大值為_____.
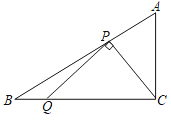
【答案】2
【解析】
過Q作QE⊥AB于E,過C作CF⊥AB于F,利用相似三角形的性質(zhì)根據(jù)一元二次方程,利用根的判別式解決問題即可.
解:過Q作QE⊥AB于E,過C作CF⊥AB于F,
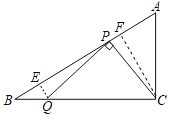
∵在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2![]() ,
,
∴∠B=30°,
∴AB=2AC=4![]() ,BC=
,BC=![]() AC=6,
AC=6,
∵∠AFC=90°,∠A=60°,
∴∠ACF=30°,
∴AF=![]() ,CF=3,
,CF=3,
設(shè)PF=x,BQ=y,
∴QE=![]() BQ=
BQ=![]() y,BE=
y,BE=![]() y,
y,
∴PE=3![]() ﹣
﹣![]() y﹣x,
y﹣x,
∵PQ⊥PC,
∴∠PEQ=∠CFP=∠CPQ=90°,
∴∠EQP+∠EPQ=∠EPQ+∠CPF=90°,
∴∠PQE=∠CPF,
∴△PEQ∽△CFP,
∴![]() ,
,
∴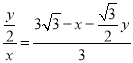
∴x2+(![]() y﹣3
y﹣3![]() )x+
)x+![]() =0,
=0,
∵方程有實(shí)數(shù)解,
∴△≥0,
∴(![]() y﹣3
y﹣3![]() )2﹣6y≥0,
)2﹣6y≥0,
整理得,y2﹣20y+36≥0,
解得y≤2或y≥18(舍棄),
∴BQ≤2,
∴BQ的最大值為2.
故答案為2.


 精英口算卡系列答案
精英口算卡系列答案 應(yīng)用題點(diǎn)撥系列答案
應(yīng)用題點(diǎn)撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的頂點(diǎn)
的頂點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
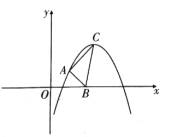
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 點(diǎn)為拋物線上異于
點(diǎn)為拋物線上異于![]() 的一點(diǎn),且
的一點(diǎn),且![]() 點(diǎn)橫、縱坐標(biāo)相等,
點(diǎn)橫、縱坐標(biāo)相等,![]() 為
為![]() 軸上任意一點(diǎn),當(dāng)
軸上任意一點(diǎn),當(dāng)![]() 取最小值時(shí),求出
取最小值時(shí),求出![]() 點(diǎn)坐標(biāo)和此時(shí)
點(diǎn)坐標(biāo)和此時(shí)![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是正方形,點(diǎn)
是正方形,點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() .
.
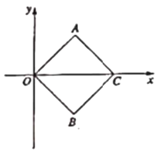
(1)正方形![]() 的邊長為 ,點(diǎn)
的邊長為 ,點(diǎn)![]() 的坐標(biāo)是 ;
的坐標(biāo)是 ;
(2)將正方形![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)
順時(shí)針旋轉(zhuǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() ,
,![]() 旋轉(zhuǎn)后的對(duì)應(yīng)點(diǎn)為
旋轉(zhuǎn)后的對(duì)應(yīng)點(diǎn)為![]() ,
,![]() ,
,![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo)及旋轉(zhuǎn)后的正方形與原正方形的重疊部分的面積;
的坐標(biāo)及旋轉(zhuǎn)后的正方形與原正方形的重疊部分的面積;
(3)動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿折線
出發(fā),沿折線![]() 方向以1個(gè)單位/秒的速度勻速運(yùn)動(dòng),同時(shí),另一動(dòng)點(diǎn)
方向以1個(gè)單位/秒的速度勻速運(yùn)動(dòng),同時(shí),另一動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿折線
出發(fā),沿折線![]() 方向以2個(gè)單位/秒的速度勻速運(yùn)動(dòng),運(yùn)動(dòng)時(shí)間為
方向以2個(gè)單位/秒的速度勻速運(yùn)動(dòng),運(yùn)動(dòng)時(shí)間為![]() 秒,當(dāng)它們相遇時(shí)同時(shí)停止運(yùn)動(dòng),當(dāng)
秒,當(dāng)它們相遇時(shí)同時(shí)停止運(yùn)動(dòng),當(dāng)![]() 為等腰三角形時(shí),求出
為等腰三角形時(shí),求出![]() 的值(直接寫出結(jié)果即可).
的值(直接寫出結(jié)果即可).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2019年11月22日,教育部發(fā)布關(guān)于《中小學(xué)教師實(shí)施教育懲戒規(guī)則(征求意見稿)》公開征求意見的通知,征求意見稿指出;教育懲戒是教師履行救育教學(xué)職責(zé)的必要手段和法定職權(quán).教育懲戒分為![]() :一般懲戒,
:一般懲戒,![]() :較重懲戒,
:較重懲戒,![]() :嚴(yán)重懲戒,
:嚴(yán)重懲戒,![]() :強(qiáng)制措施,共四個(gè)層次.為了解家長對(duì)教育懲戒的看法,某中學(xué)對(duì)學(xué)生家長進(jìn)行了隨機(jī)調(diào)查,要求每位家長選擇其中最關(guān)注的一個(gè)層次提出意見,學(xué)校對(duì)收集的信息進(jìn)行統(tǒng)計(jì),繪制了下面兩幅不完整的統(tǒng)計(jì)圖.
:強(qiáng)制措施,共四個(gè)層次.為了解家長對(duì)教育懲戒的看法,某中學(xué)對(duì)學(xué)生家長進(jìn)行了隨機(jī)調(diào)查,要求每位家長選擇其中最關(guān)注的一個(gè)層次提出意見,學(xué)校對(duì)收集的信息進(jìn)行統(tǒng)計(jì),繪制了下面兩幅不完整的統(tǒng)計(jì)圖.

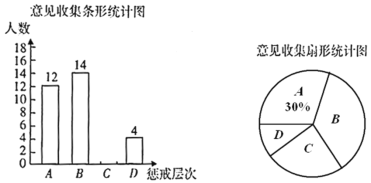
請(qǐng)你根據(jù)統(tǒng)計(jì)圖提供的信息,解答下列問題:
(1)被調(diào)查的總?cè)藬?shù)是______人;
(2)扇形統(tǒng)計(jì)圖中![]() 部分對(duì)應(yīng)的圓心角的度數(shù)為______;
部分對(duì)應(yīng)的圓心角的度數(shù)為______;
(3)補(bǔ)全條形統(tǒng)計(jì)圖;
(4)某班主任對(duì)學(xué)生進(jìn)行了紀(jì)律教育,要求小明和小軍分別從題中所述的四個(gè)層次中隨機(jī)選擇一個(gè)層次說明懲戒內(nèi)容.請(qǐng)用列表法或畫樹狀圖法求兩人選擇不同教育懲戒層次的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一艘船由A港沿北偏東60°方向航行20km至B港,然后再沿北偏西30°方向航行20km至C港.
(1)求A,C兩港之間的距離;(結(jié)果保留到0.1km)
(2)確定C港在A港的什么方向(參考數(shù)據(jù):![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
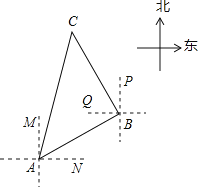
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將函數(shù)![]() 的圖象沿y軸向上平移得到一條新函數(shù)的圖象,其中點(diǎn)A(-4,m),B(-1,n),平移后的對(duì)應(yīng)點(diǎn)分別為點(diǎn)A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數(shù)表達(dá)式是 ( )
的圖象沿y軸向上平移得到一條新函數(shù)的圖象,其中點(diǎn)A(-4,m),B(-1,n),平移后的對(duì)應(yīng)點(diǎn)分別為點(diǎn)A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數(shù)表達(dá)式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
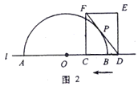
【題目】如圖1,點(diǎn)![]() 和矩形
和矩形![]() 的邊
的邊![]() 都在直線
都在直線![]() 上,以點(diǎn)
上,以點(diǎn)![]() 為圓心,以24為半徑作半圓,分別交直線
為圓心,以24為半徑作半圓,分別交直線![]() 于
于![]() 兩點(diǎn).已知:
兩點(diǎn).已知: ![]() ,
,![]() ,矩形自右向左在直線
,矩形自右向左在直線![]() 上平移,當(dāng)點(diǎn)
上平移,當(dāng)點(diǎn)![]() 到達(dá)點(diǎn)
到達(dá)點(diǎn)![]() 時(shí),矩形停止運(yùn)動(dòng).在平移過程中,設(shè)矩形對(duì)角線
時(shí),矩形停止運(yùn)動(dòng).在平移過程中,設(shè)矩形對(duì)角線![]() 與半圓
與半圓![]() 的交點(diǎn)為
的交點(diǎn)為![]() (點(diǎn)
(點(diǎn)![]() 為半圓上遠(yuǎn)離點(diǎn)
為半圓上遠(yuǎn)離點(diǎn)![]() 的交點(diǎn)).
的交點(diǎn)).
(1)如圖2,若![]() 與半圓
與半圓![]() 相切,求
相切,求![]() 的值;
的值;
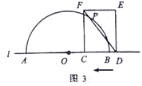
(2)如圖3,當(dāng)![]() 與半圓
與半圓![]() 有兩個(gè)交點(diǎn)時(shí),求線段
有兩個(gè)交點(diǎn)時(shí),求線段![]() 的取值范圍;
的取值范圍;
(3)若線段![]() 的長為20,直接寫出此時(shí)
的長為20,直接寫出此時(shí)![]() 的值.
的值.
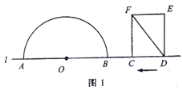
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 與x軸相交于不同的兩點(diǎn)
與x軸相交于不同的兩點(diǎn)![]() ,
,
(1)求![]() 的取值范圍
的取值范圍
(2)證明該拋物線一定經(jīng)過非坐標(biāo)軸上的一點(diǎn)![]() ,并求出點(diǎn)
,并求出點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)當(dāng)![]() 時(shí),由(2)求出的點(diǎn)
時(shí),由(2)求出的點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 構(gòu)成的
構(gòu)成的![]() 的面積是否有最值,若有,求出最值及相對(duì)應(yīng)的
的面積是否有最值,若有,求出最值及相對(duì)應(yīng)的![]() 值;若沒有,請(qǐng)說明理由.
值;若沒有,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD中,對(duì)角線AC的垂直平分線EF分別交BC,AD于點(diǎn)E,F,若BE=4,AF=6,則AC的長為( )
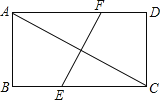
A.4![]() B.6
B.6![]() C.2
C.2![]() D.
D.![]()
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com