
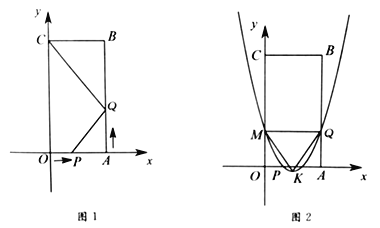
【題目】如圖1,四邊形![]() 是矩形,點
是矩形,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .點
.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒1個單位長度的速度向點
以每秒1個單位長度的速度向點![]() 運動,同時點
運動,同時點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒2個單位長度的速度向點
以每秒2個單位長度的速度向點![]() 運動,當點
運動,當點![]() 與點
與點![]() 重合時運動停止.設運動時間為
重合時運動停止.設運動時間為![]() 秒.
秒.
(1)當![]() 時,線段
時,線段![]() 的中點坐標為________;
的中點坐標為________;
(2)當![]() 與
與![]() 相似時,求
相似時,求![]() 的值;
的值;
(3)當![]() 時,拋物線
時,拋物線![]() 經過
經過![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,拋物線的頂點為
,拋物線的頂點為![]() ,如圖2所示.問該拋物線上是否存在點
,如圖2所示.問該拋物線上是否存在點![]() ,使
,使![]() ,若存在,求出所有滿足條件的
,若存在,求出所有滿足條件的![]() 點坐標;若不存在,說明理由.
點坐標;若不存在,說明理由.
【答案】(1)![]() 的中點坐標是
的中點坐標是![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】(1)先根據時間t=2,和速度可得動點P和Q的路程OP和AQ的長,再根據中點坐標公式可得結論;
(2)根據矩形的性質得:∠B=∠PAQ=90°,所以當△CBQ與△PAQ相似時,存在兩種情況:
①當△PAQ∽△QBC時,![]() ,②當△PAQ∽△CBQ時,
,②當△PAQ∽△CBQ時,![]() ,分別列方程可得t的值;
,分別列方程可得t的值;
(3)根據t=1求拋物線的解析式,根據Q(3,2),M(0,2),可得MQ∥x軸,∴KM=KQ,KE⊥MQ,畫出符合條件的點D,證明△KEQ∽△QMH,列比例式可得點D的坐標,同理根據對稱可得另一個點D.
(1)如圖1,∵點A的坐標為(3,0),
∴OA=3,
當t=2時,OP=t=2,AQ=2t=4,
∴P(2,0),Q(3,4),
∴線段PQ的中點坐標為:(![]() ,
,![]() ),即(
),即(![]() ,2);
,2);
故答案為:(![]() ,2);
,2);
(2)如圖1,∵四邊形OABC是矩形,
∴∠B=∠PAQ=90°
∴當△CBQ與△PAQ相似時,存在兩種情況:
①當△PAQ∽△QBC時,![]() ,
,
∴![]() ,
,
4t2-15t+9=0,
(t-3)(t-![]() )=0,
)=0,
t1=3(舍),t2=![]() ,
,
②當△PAQ∽△CBQ時,![]() ,
,
∴![]() ,
,
t2-9t+9=0,
t=![]() ,
,
∵0≤t≤6,![]() >7,
>7,
∴x=![]() 不符合題意,舍去,
不符合題意,舍去,
綜上所述,當△CBQ與△PAQ相似時,t的值是![]() 或
或![]() ;
;
(3)當t=1時,P(1,0),Q(3,2),
把P(1,0),Q(3,2)代入拋物線y=x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
∴拋物線:y=x2-3x+2=(x-![]() )2-
)2-![]() ,
,
∴頂點k(![]() ,-
,-![]() ),
),
∵Q(3,2),M(0,2),
∴MQ∥x軸,
作拋物線對稱軸,交MQ于E,
∴KM=KQ,KE⊥MQ,
∴∠MKE=∠QKE=![]() ∠MKQ,
∠MKQ,
如圖2,∠MQD=![]() ∠MKQ=∠QKE,設DQ交y軸于H,
∠MKQ=∠QKE,設DQ交y軸于H,
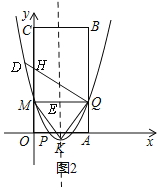
∵∠HMQ=∠QEK=90°,
∴△KEQ∽△QMH,
∴![]() ,
,
∴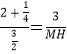 ,
,
∴MH=2,
∴H(0,4),
易得HQ的解析式為:y=-![]() x+4,
x+4,
則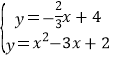 ,
,
x2-3x+2=-![]() x+4,
x+4,
解得:x1=3(舍),x2=-![]() ,
,
∴D(-![]() ,
,![]() );
);
同理,在M的下方,y軸上存在點H,如圖3,使∠HQM=![]() ∠MKQ=∠QKE,
∠MKQ=∠QKE,
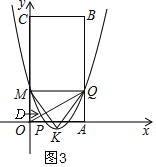
由對稱性得:H(0,0),
易得OQ的解析式:y=![]() x,
x,
則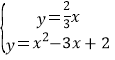 ,
,
x2-3x+2=![]() x,
x,
解得:x1=3(舍),x2=![]() ,
,
∴D(![]() ,
,![]() );
);
綜上所述,點D的坐標為:D(-![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】某商店出售網球和網球拍,網球拍每只定價80元,網球每個定價4元,商家為促銷商品,同時向客戶提供兩種優惠方案:①買一只網球拍送3個網球:②網球拍和網球都按定價的9折優惠,現在某客戶要到該商店購買球拍20只,網球![]() 個(
個(![]() 大于20).
大于20).
(1)若該客戶按優惠方案①購買需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若該客戶按優惠方案②購買需付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)若![]() 時,通過計算說明,此時按哪種優惠方案購買較為合算?
時,通過計算說明,此時按哪種優惠方案購買較為合算?
(4)當![]() 時,你能結合兩種優惠方案給出一種更為省錢的購買方案嗎?試寫出你的購買方案,并計算出所需的錢數.
時,你能結合兩種優惠方案給出一種更為省錢的購買方案嗎?試寫出你的購買方案,并計算出所需的錢數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了解該校學生的體育鍛煉情況,隨機抽查了該校部分學生一周的體育鍛煉時間的情況,并繪制了如下兩幅不完整的統計圖:
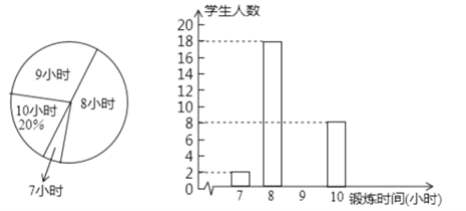
根據以上信息解答以下問題:
(1)本次抽查的學生共有多少名,并補全條形統計圖;
(2)寫出被抽查學生的體育鍛煉時間的眾數和中位數;
(3)該校一共有1800名學生,請估計該校學生一周體育鍛煉時間不低于9小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4張相同的卡片上分別寫有數字-1、-3、4、6,將卡片的背面朝上,并洗勻.
(1)從中任意抽取1張,抽到的數字是奇數的概率是 ;
(2)從中任意抽取1張,并將所取卡片上的數字記作一次函數![]() 中的
中的![]() ;再從余下的卡片中任意抽取1張,并將所取卡片上的數字記作一次函數
;再從余下的卡片中任意抽取1張,并將所取卡片上的數字記作一次函數![]() 中的
中的![]() .利用畫樹狀圖或列表的方法,求這個一次函數的圖象經過第一、二、四象限的概率.
.利用畫樹狀圖或列表的方法,求這個一次函數的圖象經過第一、二、四象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的部分圖象如圖,圖象過點(﹣1,0),對稱軸為直線
的部分圖象如圖,圖象過點(﹣1,0),對稱軸為直線![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時, ![]() 隨
隨![]() 的增大而增大.其中正確的結論有( )
的增大而增大.其中正確的結論有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店在今年2月底以每袋23元的成本價收購一批農產品準備向外銷售,當此農產品售價為每袋36元時,3月份銷售125袋,4、5月份該農產品十分暢銷,銷售量持續走高.在售價不變的基礎上,5月份的銷售量達到180袋.設4、5這兩個月銷售量的月平均增長率不變.
(1)求4、5這兩個月銷售量的月平均增長率;
(2)6月份起,該商店采用降價促銷的方式回饋顧客,經調查發現,該農產品每降價1元/袋,銷量就增加4袋,當農產品每袋降價多少元時,該商店6月份獲利1920元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民節約用水,決定實行兩級收費制度.若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價和市場價分別是多少?
(2)小明家5月份用水26噸,則他家應交水費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com