
【題目】如圖,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,還需要添加什么條件?請選擇一個加以證明
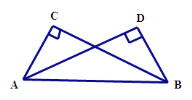
添加:
選擇:
證明:
【答案】∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD;∠CAB=∠DBA(答案不唯一),證明見解析
【解析】
根據全等三角形的各個判定定理即可得出結論,然后任取其一證明即可.
解:∵∠ACB=∠BDA=90°,AB=BA
∴若添加∠CAB=∠DBA,利用AAS即可證出△ACB≌△BDA;
若添加∠CBA=∠DAB,利用AAS即可證出△ACB≌△BDA;
若添加CA=DB,利用HL即可證出△ACB≌△BDA;
若添加BC=AD,利用HL即可證出△ACB≌△BDA;
如選擇∠CAB=∠DBA
證明:在△ACB和△BDA中
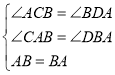
∴△ACB≌△BDA
故答案為:∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD;∠CAB=∠DBA(答案不唯一)


科目:初中數學 來源: 題型:
【題目】我們已經知道(a﹣b)2≥0,即a2﹣2ab+b2≥0.所以a2+b2≥2ab(當且僅當a=b時取等號).
閱讀1:若a、b為實數,且a>0,b>0.
∵(![]() )2≥0,∴a﹣2
)2≥0,∴a﹣2![]() +b≥0,∴a+b≥2
+b≥0,∴a+b≥2![]() (當且僅當a=b時取等號).
(當且僅當a=b時取等號).
閱讀2:若函數y=x![]() (m>0,x>0,m為常數).由閱讀1結論可知:x
(m>0,x>0,m為常數).由閱讀1結論可知:x![]() 即x
即x![]() ∴當x
∴當x![]() 即x2=m,∴x=
即x2=m,∴x=![]() (m>0)時,函數y=x
(m>0)時,函數y=x![]() 的最小值為2
的最小值為2![]() .
.
閱讀理解上述內容,解答下列問題:
問題1:當x>0時,![]() 的最小值為 ;當x<0時,
的最小值為 ;當x<0時,![]() 的最大值為 .
的最大值為 .
問題2:函數y=a+![]() (a>1)的最小值為 .
(a>1)的最小值為 .
問題3:求代數式![]() (m>﹣2)的最小值,并求出此時的m的值.
(m>﹣2)的最小值,并求出此時的m的值.
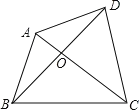
問題4:如圖,四邊形ABCD的對角線AC,BD相交于點O,△AOB、△COD的面積分別為4和16,求四邊形ABCD面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
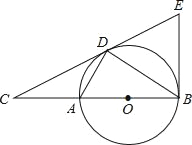
【題目】如圖,點D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.(1)判斷直線CD和⊙O的位置關系,并說明理由.
(2)過點B作⊙O的切線BE交直線CD于點E,若AC=2,⊙O的半徑是3,求∠BEC的正切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小方格都是長為1個單位的正方形.若學校位置的坐標為A(1,2),解答以下問題:
(1)請在圖中建立適當的直角坐標系,并寫出圖書館B位置的坐標;
(2)若體育館位置的坐標為C(-3,3),請在坐標系中標出體育館的位置,并順次連接學校、圖書館、體育館,得到△ABC,求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在四邊形ABCD中,AD∥BC,AD=24cm,BC=30cm,點P從A向點D以1cm/s的速度運動,到點D即停止.點Q從點C向點B以2cm/s的速度運動,到點B即停止.直線PQ將四邊形ABCD截得兩個四邊形,分別為四邊形ABQP和四邊形PQCD,則當P,Q兩點同時出發,幾秒后所截得兩個四邊形中,其中一個四邊形為平行四邊形? 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場將進貨價為30元的臺燈以40元的價格售出,平均每月能售出600個,這種臺燈的售價每上漲1元,其銷量就減少10個,
(1)為了實現銷售這種臺燈平均每月10000元的銷售利潤,售價應定為多少元?
(2)當售價定為多少元時,其銷售利潤達到最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段![]() ,
, ![]() 于點
于點![]() ,且
,且![]() ,
, ![]() 是射線
是射線![]() 上一動點,
上一動點, ![]() 、
、![]() 分別是
分別是![]() ,
, ![]() 的中點,過點
的中點,過點![]() ,
, ![]() ,
, ![]() 的圓與
的圓與![]() 的另一交點
的另一交點![]() (點
(點![]() 在線段
在線段![]() 上),連結
上),連結![]() ,
, ![]() .
.

(![]() )當
)當![]() 時,則
時,則![]() 的度數為__________.
的度數為__________.
(![]() )在點
)在點![]() 的運動過程中,當
的運動過程中,當![]() 時,取四邊形
時,取四邊形![]() 一邊的兩端點和線段
一邊的兩端點和線段![]() 上一點
上一點![]() ,若以這三點為頂點的三角形是直角三角形,當
,若以這三點為頂點的三角形是直角三角形,當![]() 時,則
時,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
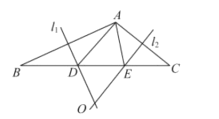
【題目】如圖,在△ABC中,邊AB的垂直平分線OM與邊AC的垂直平分線ON交于點O,分別交BC于點D、E,已知△ADE的周長5cm.
(1)求BC的長;
(2)分別連接OA、OB、OC,若△OBC的周長為13cm,求OA的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
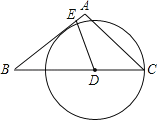
【題目】如圖,在等腰△ABC中,AB=AC=5,BC=6,點D為BC邊上一動點(不與點B重合),過D作射線DE交AB邊于E,使∠BDE=∠A,以D為圓心、DC的長為半徑作⊙D.
(1)設BD=x,AE=y,求y關于x的函數關系式,并寫出定義域.
(2)當⊙D與AB邊相切時,求BD的長.
(3)如果⊙E是以E為圓心,AE的長為半徑的圓,那么當BD的長為多少時,⊙D與⊙E相切?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com