
【題目】在求1+2+22+23+24+25+26的值時,小明發現:從第二個加數起每一個加數都是前一個加數的2倍,于是他設:S=1+2+22+23+24+25+26①然后在①式的兩邊都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
【答案】(1)1093.5(2)![]()
【解析】
試題(1)將1+3+32+33+34+35+36乘3,減去1+3+32+33+34+35+36,把它們的結果除以3﹣1=2即可求解;
(2)將1+a+a2+a3+…+a2013乘a,減去1+a+a2+a3+…+a2013,把它們的結果除以a﹣1即可求解.
試題解析:解:(1)1+3+32+33+34+35+36
=[(1+3+32+33+34+35+36)×3﹣(1+3+32+33+34+35+36)]÷(3﹣1)
=[(3+32+33+34+35+36+37)﹣(1+3+32+33+34+35+36)]÷2
=(37﹣1)÷2
=2187÷2
=1093.5;
(2)1+a+a2+a3+…+a2013(a≠0且a≠1)
═[(1+a+a2+a3+…+a2013)×a﹣(1+a+a2+a3+…+a2013)]÷(a﹣1)
=[(a+a2+a3+…+a2013+a2014)﹣(1+a+a2+a3+…+a2013)]÷(a﹣1)
=(a2014﹣1)÷(a﹣1)
=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,四邊形ABCD是正方形,AB=4,點G在BC邊上,BG=3,DE⊥AG于點E,BF⊥AG于點F.
(1)求BF和DE的長;
(2)如圖2,連接DF、CE,探究并證明線段DF與CE的數量關系與位置關系.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正方體骰子(相對面上的點數分別為1和6、2和5、3和4)放置于水平桌面上,如圖1。在圖2中,將骰子向右翻滾90°,然后在桌面上按逆時針方向旋轉90°,則完成一次變換。若骰子的初始位置為圖1所示的狀態,那么按上述規則連續完成14次變換后,骰子朝上一面的點數是_____________________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是AB上一點,DF交AC于點E,FC∥AB,則下列結論錯誤的是( )

A. 若AE=CE,則DE=FE B. 若DE=FE,則AE=CE
C. 若BC=CF,則AD=CF D. 若AD=CF,則DE=FE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,解答問題.
飲水問題是關系到學生身心健康的重要生活環節,東坡中學共有教學班24個,平均每班有學生50人,經估算,學生一年在校時間約為240天(除去各種節假日),春、夏、秋、冬季各60天.原來,學生飲水一般都是購純凈水(其他碳酸飲料或果汁價格更高),純凈水零售價為1.5元/瓶,每個學生春、秋、冬季平均每天買1瓶純凈水,夏季平均每天要買2瓶純凈水,學校為了減輕學生消費負擔,要求每個班自行購買1臺冷熱飲水機,經調查,購買一臺功率為500 W的冷熱飲水機約為150元,純凈水每桶6元,每班春、秋兩季,平均每1.5天購買4桶,夏季平均每天購買5桶,冬季平均每天購買1桶,飲水機每天開10小時,當地民用電價為0.50元/度.
問題:
(1)在未購買飲水機之前,全年平均每個學生要花費多少錢來購買純凈水飲用?
(2)在購買飲水機解決學生飲水問題后,每班當年共要花費多少元?
(3)這項便利學生的措施實施后,東坡中學當年全體學生共節約多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為2,E是BC的中點,以點A為中心,把△ABE逆時針旋轉90°,設點E的對應點為F. 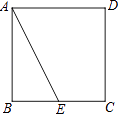
(1)畫出旋轉后的三角形.
(2)在(1)的條件下,
①求EF的長;
②求點E經過的路徑弧EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】88層的金茂大廈的電梯上,有顯示樓層的液晶屏,如圖,可顯示01,02,…,88,由于屏幕受到損壞,顯示左邊數字的7根線段中有1根不能亮了,顯示右邊數字的7根線段中有3根不能亮了。請問:電梯在運行的過程中,最多還有 _____個樓層的數字顯示是正確的.

(說明)數字0、1、2、3、4、5、6、7、8、9顯示方式如下圖所示.

![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,E是AB的中點,連接DE并延長交CB的延長線于點F,點G在邊BC上,且∠GDF=∠ADF.連接EG,判斷EG與DF的位置關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸是初中數學教材中數形結合的第一個實例,它包括原點,正方向和長度單位三要素,每一個實數都可以用數軸上的一個點來表示.
![]() 數軸上某一個點所對應的數為
數軸上某一個點所對應的數為![]() ,另一個點對應的數為
,另一個點對應的數為![]() ,則這兩點之間的距離為________;
,則這兩點之間的距離為________;
![]() 數軸上的數
數軸上的數![]() 對應的點為
對應的點為![]() ,點
,點![]() 位于
位于![]() 點的右邊,距
點的右邊,距![]() 點
點![]() 個長度單位,
個長度單位,![]() 為線段
為線段![]() 上的一點,
上的一點,![]() ,電子螞蟻
,電子螞蟻![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發,相向而行,
同時出發,相向而行,![]() 的速度為
的速度為![]() 個長度單位/秒,
個長度單位/秒,![]() 的速度為
的速度為![]() 個長度單位/秒.
個長度單位/秒.
①當![]() 、
、![]() 距
距![]() 點距離相同時,求運動時間
點距離相同時,求運動時間![]() ;
;
②若電子螞蟻![]() 通過
通過![]() 點
點![]() 秒后與電子螞蟻
秒后與電子螞蟻![]() 相遇,求
相遇,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com