
【題目】數軸是初中數學教材中數形結合的第一個實例,它包括原點,正方向和長度單位三要素,每一個實數都可以用數軸上的一個點來表示.
![]() 數軸上某一個點所對應的數為
數軸上某一個點所對應的數為![]() ,另一個點對應的數為
,另一個點對應的數為![]() ,則這兩點之間的距離為________;
,則這兩點之間的距離為________;
![]() 數軸上的數
數軸上的數![]() 對應的點為
對應的點為![]() ,點
,點![]() 位于
位于![]() 點的右邊,距
點的右邊,距![]() 點
點![]() 個長度單位,
個長度單位,![]() 為線段
為線段![]() 上的一點,
上的一點,![]() ,電子螞蟻
,電子螞蟻![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發,相向而行,
同時出發,相向而行,![]() 的速度為
的速度為![]() 個長度單位/秒,
個長度單位/秒,![]() 的速度為
的速度為![]() 個長度單位/秒.
個長度單位/秒.
①當![]() 、
、![]() 距
距![]() 點距離相同時,求運動時間
點距離相同時,求運動時間![]() ;
;
②若電子螞蟻![]() 通過
通過![]() 點
點![]() 秒后與電子螞蟻
秒后與電子螞蟻![]() 相遇,求
相遇,求![]() 的值.
的值.
![]()
科目:初中數學 來源: 題型:
【題目】在求1+2+22+23+24+25+26的值時,小明發現:從第二個加數起每一個加數都是前一個加數的2倍,于是他設:S=1+2+22+23+24+25+26①然后在①式的兩邊都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,⊙C的半徑為r,P是與圓心C不重合的點,點P關于⊙C的限距點的定義如下:若P′為直線PC與⊙C的一個交點,滿足r≤PP′≤2r,則稱P′為點P關于⊙C的限距點,如圖為點P及其關于⊙C的限距點P′的示意圖. 
(1)當⊙O的半徑為1時.
①分別判斷點M(3,4),N( ![]() ,0),T(1,
,0),T(1, ![]() )關于⊙O的限距點是否存在?若存在,求其坐標;
)關于⊙O的限距點是否存在?若存在,求其坐標;
②點D的坐標為(2,0),DE,DF分別切⊙O于點E,點F,點P在△DEF的邊上.若點P關于⊙O的限距點P′存在,求點P′的橫坐標的取值范圍;
(2)保持(1)中D,E,F三點不變,點P在△DEF的邊上沿E→F→D→E的方向運動,⊙C的圓心C的坐標為(1,0),半徑為r,請從下面兩個問題中任選一個作答.
問題1 | 問題2 |
若點P關于⊙C的限距點P′存在,且P′隨點P的運動所形成的路徑長為πr,則r的最小值為 | 若點P關于⊙C的限距點P′不存在,則r的取值范圍為 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,BE平分∠ABC交AD于點E,F為BE上一點,連接DF,過F作FG⊥DF交BC于點G,連接BD交FG于點H,若FD=FG,BF=3 ![]() ,BG=4,則GH的長為 .
,BG=4,則GH的長為 . 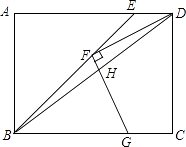
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為原點,直線AB分別與x軸、y軸交于點B和A,與反比例函數的圖象交于C、D,CE⊥x軸于點E,若tan∠ABO= ![]() ,OB=4,OE=2,點D的坐標為(6,m).
,OB=4,OE=2,點D的坐標為(6,m). 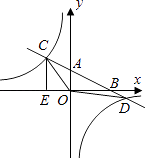
(1)求直線AB和反比例函數的解析式;
(2)求△OCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著手機的普及,微信![]() 一種聊天軟件
一種聊天軟件![]() 的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況
的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況![]() 超額記為正,不足記為負
超額記為正,不足記為負![]() 單位:斤
單位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
與計劃量的差值 |
|
|
|
|
|
|
|
(1)根據記錄的數據可知前三天共賣出 ______ 斤;
(2)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售 ______ 斤;
(3)本周實際銷售總量達到了計劃數量沒有?
(4)若冬季每斤按8元出售,每斤冬棗的運費平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板按如圖所示的方式擺放,其中△ABC為含有45°角的三角板,直線AD是等腰直角三角板的對稱軸,且斜邊上的點D為另一塊三角板DMN的直角頂點,DM、DN分別交AB、AC于點E、F.則下列四個結論:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四邊形AEDF=![]() BC2.其中正確結論是_____(填序號).
BC2.其中正確結論是_____(填序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列方程中變形正確的是( )
①3x+6=0變形為x+2=0;
②2x+8=5-3x變形為x=3;
③![]() +
+![]() =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;
④(x+2)-2(x-1)=0去括號,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、C、N三點在同一直線上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,則∠BCM:∠BCN=_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com