
【題目】問題探究
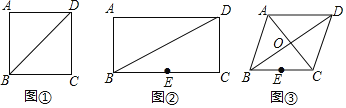
![]() 請在圖
請在圖![]() 的正方形ABCD的對角線BD上作一點P,使
的正方形ABCD的對角線BD上作一點P,使![]() 最小;
最小;
![]() 如圖
如圖![]() ,點P為矩形ABCD的對角線BD上一動點,
,點P為矩形ABCD的對角線BD上一動點,![]() ,
,![]() ,點E為BC邊的中點,請作一點P,使
,點E為BC邊的中點,請作一點P,使![]() 最小,并求這個最小值;
最小,并求這個最小值;
問題解決
![]() 如圖
如圖![]() ,李師傅有一塊邊長為1000米的菱形采摘園ABCD,
,李師傅有一塊邊長為1000米的菱形采摘園ABCD,![]() 米,BD為小路,BC的中點E為一水池,李師傅現在準備在小路BD上建一個游客臨時休息納涼室P,為了節省土地,使休息納涼室P到水池E與大門C的距離之和最短,那么是否存在符合條件的點P?若存在,請作出點P的位置,并求出這個最短距離;若不存在,請說明理由.
米,BD為小路,BC的中點E為一水池,李師傅現在準備在小路BD上建一個游客臨時休息納涼室P,為了節省土地,使休息納涼室P到水池E與大門C的距離之和最短,那么是否存在符合條件的點P?若存在,請作出點P的位置,并求出這個最短距離;若不存在,請說明理由.
【答案】解:![]() 見解析
見解析![]()
![]() 的最小值為3;
的最小值為3;![]() 存在,且最短距離約為985米
存在,且最短距離約為985米
【解析】
(1)利用兩點之間線段最短,即可得出結論;
(2)先確定出點P的位置,再求出∠CBD=30°,進而判斷出△BCC'是等邊三角形,即可得出結論;
(3)先確定出點P的位置,再求出OA,OB,進而利用面積求出AH,最后用勾股定理即可得出結論.
解:![]() 如圖
如圖![]() ,連接AC交BD于點P,則點P就是所要求作的點,
,連接AC交BD于點P,則點P就是所要求作的點,
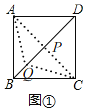
理由:在BD上任取一點異于點P的點Q,連接AQ,CQ,
![]() ;
;
![]() 如圖
如圖![]()
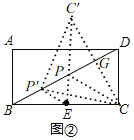 ,
,
作點C關于BD的對稱點C',連接EC'交BD于點P,連接C'P,
∵點C與點C'關于BD的對稱點,
∴CP=C'P,
∴C'P+PE=C'P'+P'E=C'E,
在BD上任取異于點P的P',連接P'E,P'C,C'P',
∴C'P'+P'E=P'C+P'E>C'E,
∴點P就是所要求作的點,EC'的長度PE+PC的最小值,
∵四邊形ABCD是矩形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∵點C和點C'關于BD對稱,
設CC'交BD于G,
∴BD是CC'的垂直平分線,連接BC',
∴∠C'BD=∠CBD=30°,BC'=BC,
∴∠C'BC=60°,
∴△BCC'是等邊三角形,
∵點E是BC的中點,
∴CE⊥BC,
![]() ,
,
![]() ,
,
即:![]() 的最小值為3;
的最小值為3;
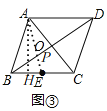
![]() 存在,如圖
存在,如圖![]() ,連接AE交BD于P,點P就是所要求作的點,AE的長度就是休息納涼室P到水池E與大門C的距離之和最短的值,
,連接AE交BD于P,點P就是所要求作的點,AE的長度就是休息納涼室P到水池E與大門C的距離之和最短的值,
 ,
,
![]() 四邊形ABCD是菱形,
四邊形ABCD是菱形,
![]() 點C關于BD的對稱點為A,連接AE,交BD于P,點P就是所要求作的點,
點C關于BD的對稱點為A,連接AE,交BD于P,點P就是所要求作的點,
![]() 米,
米,![]() 米,
米,![]() 于Q,
于Q,
![]() 米,
米,![]() 米,
米,
過點A作![]() 于H,
于H,
![]() ,
,
![]() 米,
米,
在![]() 中,根據勾股定理得,
中,根據勾股定理得,![]() 米,
米,
![]() 米,
米,
在![]() 中,
中,![]() 米,
米,
即:存在點P,且最短距離約為985米.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某景區的三個景點A、B、C在同一線路上.甲、乙兩名游客從景點A出發,甲步行到景點C;乙乘景區觀光車先到景點B,在B處停留一段時間后,再步行到景點C,甲、乙兩人同時到達景點C.甲、乙兩人距景點A的路程y(米)與甲出發的時間x(分)之間的函數圖象如圖所示.

(1)乙步行的速度為_ __米/分.
(2)求乙乘景區觀光車時y與x之間的函數關系式.
(3)甲出發多長時間與乙第一次相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
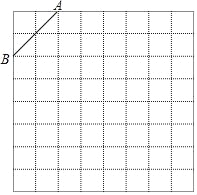
【題目】如圖是規格為8×8的正方形網格,請在所給網格中按下列要求操作:
(1)在網格中建立平面直角坐標系,使A點坐標為(﹣2,4),B點坐標為(﹣4,2);
(2)在第二象限內的格點上畫一點C,使點C與線段AB組成一個以AB為底的等腰三角形,且腰長是無理數,則C點坐標是 ;
(3)求△ABC中BC邊上的高長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,某乘客乘高速列車從甲地經過乙地到丙地,列車勻速行駛,圖②為列車離乙地路程y(千米)與行駛時間x(小時)的函數關系圖象.
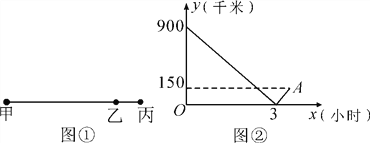
(1)填空:甲、丙兩地距離_______千米;
(2)求高速列車離乙地的路程y與行駛時間x之間的函數關系式,并寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BC=EC,∠BCE=∠ACD,如果只添加一個條件,使△ABC ≌ △DEC,則添加的條件不能為( )
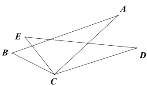
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
情形展示:
情形一:如圖![]() ,在
,在![]() 中,沿等腰三角形ABC的頂角
中,沿等腰三角形ABC的頂角![]() 的平分線
的平分線![]() 折疊,若點B與點C重合,則稱
折疊,若點B與點C重合,則稱![]() 是
是![]() 的“好角”,如圖
的“好角”,如圖![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分線
的平分線![]() 折疊,剪掉重復部分,再將余下部分沿
折疊,剪掉重復部分,再將余下部分沿![]() 的平分線
的平分線![]() 折疊,若點
折疊,若點![]() 與點C重合,則稱
與點C重合,則稱![]() 是
是![]() 的“好角”.
的“好角”.
情形二:如圖![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分線
的平分線![]() 折疊,剪掉重復部分,再將余下部分沿
折疊,剪掉重復部分,再將余下部分沿![]() 的平分線
的平分線![]() 折疊,剪掉重復部分
折疊,剪掉重復部分![]() 重復折疊n次,最終若點
重復折疊n次,最終若點![]() 與點C重合,則稱
與點C重合,則稱![]() 是
是![]() 的“好角”,探究發現:
的“好角”,探究發現:![]() 不妨設
不妨設![]()
![]() 如圖
如圖![]() ,若
,若![]() 是
是![]() 的“好角”,則
的“好角”,則![]() 與
與![]() 的數量關系是:______.
的數量關系是:______.
![]() 如圖
如圖![]() ,若
,若![]() 是
是![]() 的“好角”,則
的“好角”,則![]() 與
與![]() 的數量關系是:______.
的數量關系是:______.
![]() 如圖
如圖![]() ,若
,若![]() 是
是![]() 的“好角”,則
的“好角”,則![]() 與
與![]() 的數量關系是:______.
的數量關系是:______.
應用提升:
![]() 如果一個三角形的三個角分別為
如果一個三角形的三個角分別為![]() ,
,![]() ,
,![]() ,我們發現
,我們發現![]() 和
和![]() 的兩個角都是此三角形的“好角”;如果有一個三角形,它的三個角均是此三角形的“好角”,且已知最小的角是
的兩個角都是此三角形的“好角”;如果有一個三角形,它的三個角均是此三角形的“好角”,且已知最小的角是![]() ,求另外兩個角的度數.
,求另外兩個角的度數.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠A=∠B,AE=BE,點D在AC邊上,∠1=∠2,AE和BD相交于點O.
(1)求證:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com