
【題目】四邊形一條對角線所在直線上的點,如果到這條對角線的兩端點的距離不相等,但到另一對角線的兩個端點的距離相等,則稱這點為這個四邊形的準等距點.如圖,點P為四邊形ABCD對角線AC所在直線上的一點,PD=PB,PA≠PC,則點P為四邊形ABCD的準等距點. 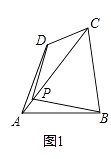
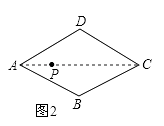
(1)如圖2,畫出菱形ABCD的一個準等距點. 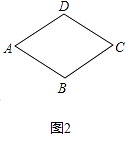
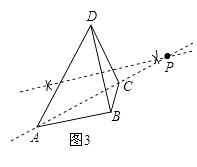
(2)如圖3,作出四邊形ABCD的一個準等距點(尺規作圖,保留作圖痕跡,不要求寫作法). 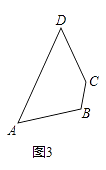
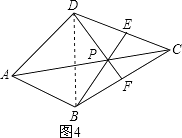
(3)如圖4,在四邊形ABCD中,P是AC上的點,PA≠PC,延長BP交CD于點E,延長DP交BC于點F,且∠CDF=∠CBE,CE=CF.求證:點P是四邊形ABCD的準等距點. 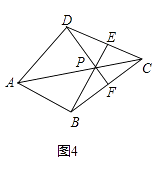
【答案】
(1)解:如圖2,點P即為所畫點.
(2)解:如圖3,點P即為所作點
(3)解:證明:連接DB,
在△DCF與△BCE中, 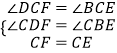 ,
,
∴△DCF≌△BCE(AAS),
∴CD=CB,
∴∠CDB=∠CBD.
∴∠PDB=∠PBD,
∴PD=PB,
∵PA≠PC
∴點P是四邊形ABCD的準等距點
【解析】(1)根據菱形的性質,在菱形對角線上找出除中心外的任意一點即可;(2)作對角線BD的垂直平分線于與另一對角線AC相交于點P,根據線段垂直平分線上的點到線段兩端點的距離相等可得點P即為所求的準等距點;(3)連接BD,先利用“角角邊”證明△DCF和△BCE全等,根據全等三角形對應邊相等可得CD=CB,再根據等邊對等角的性質可得∠CDB=∠CBD,從而得到∠PDB=∠PBD,然后根據等角對等邊的性質可得PD=PB,根據準等距點的定義即可得證.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c經過A(﹣3.0)、C(0,4),點B在拋物線上,CB∥x軸,且AB平分∠CAO.
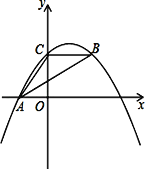
(1)求拋物線的解析式a,b,c;
(2)線段AB上有一動點P,過點P作y軸的平行線,交拋物線于點Q,求線段PQ的最大值;
(3)拋物線的對稱軸上是否存在點M,使△ABM是以AB為直角邊的直角三角形?如果存在求出點M坐標;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班有48位同學,在一次數學檢測中,分數只取整數,統計其成績,繪制出頻數分布直方圖(橫半軸表示分數,把50.5分到100.5分之間的分數分成5組,組距是10分,縱半軸表示頻數)如圖所示,從左到右的小矩形的高度比是1:3:6:4:2,則由圖可知,其中分數在70.5~80.5之間的人數是( )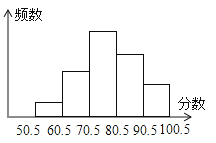
A.9
B.18
C.12
D.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com