
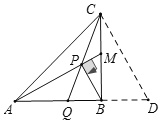
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一點,連接
上一點,連接![]()
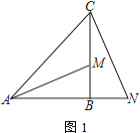
(1)如圖1,若![]() ,
,![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 與
與![]() 垂直,求證:
垂直,求證:![]()
(2)過點![]() 作
作![]() ,
,![]() 為垂足,連接
為垂足,連接![]() 并延長交
并延長交![]() 于點
于點![]() .
.
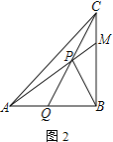
①如圖2,若![]() ,求證:
,求證:![]()
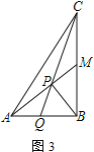
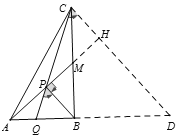
②如圖3,若![]() 是
是![]() 的中點,直接寫出
的中點,直接寫出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
【答案】(1)證明見解析;(2)①證明見解析;②![]()
【解析】
(1)延長![]() 交
交![]() 于點
于點![]() ,證明
,證明![]() 即可得;
即可得;
(2)①過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,由(1),得
,由(1),得![]() ,再根據平行線分線段成比例定理即可得到結論;
,再根據平行線分線段成比例定理即可得到結論;
②過點C作CD//BP交AB的延長線于點D,延長AM交CD于點H,先證明△BPM≌△CHM,從而可得BP=CH,PM=HM,再證明△ABM∽△BPM,得到![]() ,在Rt△PCH中,由tan∠PCH=
,在Rt△PCH中,由tan∠PCH=![]() 可得tan∠BPQ=
可得tan∠BPQ=![]() ,繼而根據BC=2BM,
,繼而根據BC=2BM,![]() 即可求得答案.
即可求得答案.
(1)延長![]() 交
交![]() 于點
于點![]() ,
,
∵![]() 與
與![]() 垂直,
垂直,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,
,
∵![]() ,∴
,∴![]() 與
與![]() 垂直,
垂直,
由(1),得![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ;
;
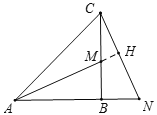
②過點C作CD//BP交AB的延長線于點D,延長AM交CD于點H,
∴∠PCH=∠BPQ,
∵![]() ,∴
,∴![]() ⊥
⊥![]() ,
,
∴∠BPM=∠CHM=90°,
又∵∠BMP=∠CMH,BM=CM,
∴△BPM≌△CHM,
∴BP=CH,PM=HM,
∴PH=2PM,
∵∠PMB=∠BMA,∠ABM=∠BPM=90°,
∴△ABM∽△BPM,
∴![]() ,
,
在Rt△PCH中,tan∠PCH=![]() ,
,
∴tan∠BPQ=![]() ,
,
又∵BC=2BM,![]() ,
,
∴tan∠BPQ=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
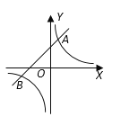
【題目】如圖,反比例函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點.
兩點.
求:(1)反比例函數關系式;
(2)n的值;
(3)一次函數關系式;
(4)根據圖像回答,當反比例函數的值大于一次函數的值時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場同時購進甲、乙兩種商品共100件,其進價和售價如下表:
商品名稱 | 甲 | 乙 |
進價(元/件) | 40 | 90 |
售價(元/件) | 60 | 120 |
設其中甲種商品購進x件,商場售完這100件商品的總利潤為y元.
(Ⅰ)寫出y關于x的函數關系式;
(Ⅱ)該商場計劃最多投入8000元用于購買這兩種商品,
①至少要購進多少件甲商品?
②若銷售完這些商品,則商場可獲得的最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017山東日照)已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=2,與x軸的一個交點坐標為(4,0),其部分圖象如圖所示,下列結論:
①拋物線過原點;
②4a+b+c=0;
③a﹣b+c<0;
④拋物線的頂點坐標為(2,b);
⑤當x<2時,y隨x增大而增大.
其中結論正確的是( )

A. ①②③ B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,其中
兩點,其中![]() ,
,![]() .該拋物線與
.該拋物線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于另一點
軸交于另一點![]() .
.

(1)求![]() 的值及該拋物線的解析式;
的值及該拋物線的解析式;
(2)如圖2.若點![]() 為線段
為線段![]() 上的一動點(不與
上的一動點(不與![]() 重合).分別以
重合).分別以![]() 、
、![]() 為斜邊,在直線
為斜邊,在直線![]() 的同側作等腰直角△
的同側作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,連接
,連接![]() ,試確定△
,試確定△![]() 面積最大時
面積最大時![]() 點的坐標.
點的坐標.
(3)如圖3.連接![]() 、
、![]() ,在線段
,在線段![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 為頂點的三角形與△
為頂點的三角形與△![]() 相似,若存在,請直接寫出點
相似,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三位數的百位上的數字減去十位上的數字等于其個位上的數字,則稱這個三位數為“差數”,同時,如果百位上的數字為![]() 、十位上的數字為
、十位上的數字為![]() ,三位數
,三位數![]() 是“差數”,我們就記:
是“差數”,我們就記:![]() ,其中,
,其中,![]() ,
,![]() .例如三位數514.∵
.例如三位數514.∵![]() ,∴514是“差數”,∴
,∴514是“差數”,∴![]() .
.
(1)已知一個三位數![]() 的百位上的數字是6,若
的百位上的數字是6,若![]() 是“差數”,
是“差數”,![]() ,求
,求![]() 的值;
的值;
(2)求出小于300的所有“差數”的和,若這個和為![]() ,請判斷
,請判斷![]() 是不是“差數”,若是,請求出
是不是“差數”,若是,請求出![]() ;若不是,請說明理由.
;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
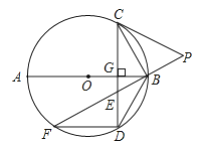
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 于點
于點![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,延長
,延長![]() 至點
至點![]() ,連接
,連接![]() ,使
,使![]() ,延長
,延長![]() 與
與![]() 交于點
交于點![]() ,連結
,連結![]() ,
,![]() .
.
(1)連結![]() ,求證:
,求證:![]() ;
;
(2)求證:![]() 是
是![]() 的切線;
的切線;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】日照間距系數反映了房屋日照情況.如圖①,當前后房屋都朝向正南時,日照間距系數=L:(H﹣H1),其中L為樓間水平距離,H為南側樓房高度,H1為北側樓房底層窗臺至地面高度.
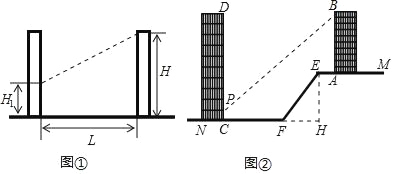
如圖②,山坡EF朝北,EF長為15m,坡度為i=1:0.75,山坡頂部平地EM上有一高為22.5m的樓房AB,底部A到E點的距離為4m.
(1)求山坡EF的水平寬度FH;
(2)欲在AB樓正北側山腳的平地FN上建一樓房CD,已知該樓底層窗臺P處至地面C處的高度為0.9m,要使該樓的日照間距系數不低于1.25,底部C距F處至少多遠?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有4個標有1,2,3,4的小球,它們形狀、大小完全相同.小明從盒子里隨機取出一個小球,記下球上的數字,作為點P的橫坐標x,放回然后再隨機取出一個小球,記下球上的數字,作為點P的縱坐標y.
(1)畫樹狀圖或列表,寫出點P所有可能的坐標;
(2)求出點P在以原點為圓心,5為半徑的圓上的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com