
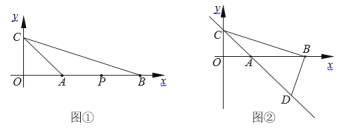
【題目】定義:點P在△ABC的邊上,且與△ABC的頂點不重合.若滿足△PAB、△PBC、△PAC至少有一個三角形與△ABC相似(但不全等),則稱點P為△ABC的自相似點.如圖①,已知點A、B、C的坐標分別為(1,0)、(3,0)、(0,1).
(1)若點P的坐標為(2,0),求證點P是△ABC的自相似點;
(2)求除點(2,0)外△ABC所有自相似點的坐標;
(3)如圖②,過點B作DB⊥BC交直線AC于點D,在直線AC上是否存在點G,使△GBD與△GBC有公共的自相似點?若存在,請舉例說明;若不存在,請說明理由.
【答案】(1)見解析;(2)△CPA∽△CAB,此時P(![]() ,
,![]() );△BPA∽△BAC,此時P(
);△BPA∽△BAC,此時P(![]() ,
,![]() );(3)S(3,-2)是△GBD與△GBC公共的自相似點,見解析
);(3)S(3,-2)是△GBD與△GBC公共的自相似點,見解析
【解析】
(1)利用:兩邊對應成比例且夾角相等,證明△APC∽△CAB即可;
(2)分類討論:△CPA∽△CAB和△BPA∽△BAC,分別求得P點的坐標;
(3)先求得點D的坐標,說明點G(5,![]() )、S(3,-2)在直線AC:
)、S(3,-2)在直線AC:![]() 上,證得△ABC
上,證得△ABC![]() △SGB,再證得△GBS∽△GCB,說明點S是△GBC的自相似點;又證得△DBG
△SGB,再證得△GBS∽△GCB,說明點S是△GBC的自相似點;又證得△DBG![]() △DSB,說明點S是△GBD的自相似點.從而說明S(3,-2)是△GBD與△GBC公共的自相似點.
△DSB,說明點S是△GBD的自相似點.從而說明S(3,-2)是△GBD與△GBC公共的自相似點.
(1)如圖,
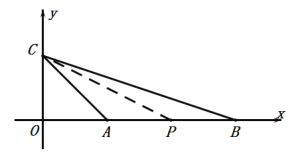
∵A(1,0),B(3,0),C(0,1),P(2,0),
∴AP=2-1=1,
AC=![]()
![]() ,
,
AB=3-1=2,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
∵∠PAC=∠CAB,
∴△APC∽△CAB,
故點P是△ABC的自相似點;
(2)點P只能在BC上,
①△CPA∽△CAB,如圖,
由(1)得:AC![]()
![]() ,AB
,AB![]() ,
,
又![]() ,
,
∵△CPA∽△CAB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
過點P作PD∥y軸交![]() 軸于D,
軸于D,
∴![]() ,
,![]() ,
,
∴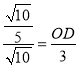 ,
,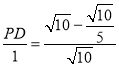 ,
,
∴![]() ,
,![]() ,
,
![]() P點的坐標為(
P點的坐標為(![]() ,
,![]() )
)
②△BPA∽△BAC,如圖,

由前面獲得的數據:AB![]() ,
,![]() ,
,
∵△BPA∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
過點P作PE∥y軸交![]() 軸于E,
軸于E,
∴![]() ,
,
∴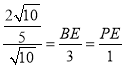 ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() P點的坐標為(
P點的坐標為(![]() ,
,![]() );
);
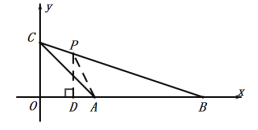
(3)存在.當點G的坐標為(5,![]() )時,△GBD與△GBC公共的自相似點為S(3,
)時,△GBD與△GBC公共的自相似點為S(3,![]() ).理由如下:
).理由如下:
如圖:
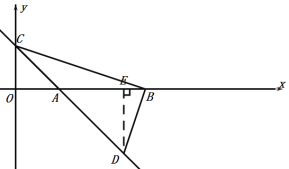
設直線AC的解析式為:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直線AC的解析式為:![]() ,
,
過點D作DE⊥x軸于點E,
∵∠CBO+∠DBE=90![]() ,∠EDB+∠DBE=90
,∠EDB+∠DBE=90![]() ,
,
∴∠CBO=∠EDB,
∴![]() ,
,
∴![]() ,
,
設BE=a,則DE=3a,
∴OE=3-a,
∴點D的坐標為(3-a,-3a) ,
∵點D在直線AC上,
∴![]() ,
,
解得:![]() ,
,
∴點D的坐標為(![]() ,
,![]() ) ;
) ;

如下圖:當點G的坐標為(5,![]() )時,△GBD與△GBC公共的自相似點為S(3,
)時,△GBD與△GBC公共的自相似點為S(3,![]() ).
).
直線AC的解析式為:![]() ,
,
∵![]() ,
,![]() ,
,
∴點G、點S在直線AC上,
過點G作GH⊥x軸于點H,
∵![]() ,
,
∴![]() ,
,
由S(3,![]() )、B(3,0)知BS⊥x軸,
)、B(3,0)知BS⊥x軸,
∴△AED、△ABS、△AHG為等腰直角三角形,
∵D (![]() ,
,![]() ),S
),S![]() ,G(
,G(![]() ,
,
∴![]() ,
,![]() ,B
,B![]() ,
,
 ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
在△ABC和△SGB中
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
![]()
∴![]()
∴△ABC![]() △SGB
△SGB
∴∠SBG=∠BCA,
又∠SGB=∠BGC,
∴△GBS∽△GCB,
∴點S是△GBC的自相似點;
在△DBG和△DSB中,
∵ ,
, ,
,
∴![]() ,且
,且![]() ,
,
∴△DBG![]() △DSB;
△DSB;
∴點S是△GBD的自相似點.
∴S(3,![]() )是△GBD與△GBC公共的自相似點.
)是△GBD與△GBC公共的自相似點.



 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】閱讀以下材料,并按要求完成相應地任務:
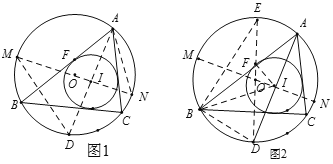
萊昂哈德·歐拉(Leonhard Euler)是瑞士數學家,在數學上經常見到以他的名字命名的重要常數,公式和定理,下面是歐拉發現的一個定理:在△ABC中,R和r分別為外接圓和內切圓的半徑,O和I分別為其外心和內心,則![]() .
.
如圖1,⊙O和⊙I分別是△ABC的外接圓和內切圓,⊙I與AB相切分于點F,設⊙O的半徑為R,⊙I的半徑為r,外心O(三角形三邊垂直平分線的交點)與內心I(三角形三條角平分線的交點)之間的距離OI=d,則有d2=R2﹣2Rr.
下面是該定理的證明過程(部分):
延長AI交⊙O于點D,過點I作⊙O的直徑MN,連接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所對的圓周角相等),
∴△MDI∽△ANI,
∴![]() ,
,
∴![]() ①,
①,
如圖2,在圖1(隱去MD,AN)的基礎上作⊙O的直徑DE,連接BE,BD,BI,IF,
∵DE是⊙O的直徑,∴∠DBE=90°,
∵⊙I與AB相切于點F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所對圓周角相等),
∴△AIF∽△EDB,
∴![]() ,∴
,∴![]() ②,
②,
任務:(1)觀察發現:![]() ,
,![]() (用含R,d的代數式表示);
(用含R,d的代數式表示);
(2)請判斷BD和ID的數量關系,并說明理由;
(3)請觀察式子①和式子②,并利用任務(1),(2)的結論,按照上面的證明思路,完成該定理證明的剩余部分;
(4)應用:若△ABC的外接圓的半徑為5cm,內切圓的半徑為2cm,則△ABC的外心與內心之間的距離為 cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,∠ABC的角平分線BE與AD交于點E,∠BED的角平分線EF與DC交于點F,若AB=8,DF=3FC,則BC=__________.
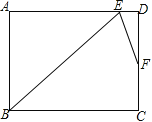
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市有2000名學生參加了2018年全省八年級數學學業水平測試.其中有這樣一題:如圖,分別以線段BD的端點B、D為圓心,相同的長為半徑畫弧,兩弧相交于A、C兩點,連接AB、AD、CB、CD.若AB=2,BD=2![]() ,求四邊形ABCD的面積.
,求四邊形ABCD的面積.

統計我市學生解答和得分情況,并制作如下圖表:

(1)求學業水平測試中四邊形ABCD的面積;
(2)請你補全條形統計圖;
(3)我市該題的平均得分為多少?
(4)我市得3分以上的人數為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形網格中,點A(3,4),⊙A的半徑為![]() .
.
(1)請在網格中畫出⊙A;
(2)請標出⊙A上的三個相鄰的格點B1、B2、B3,連接B1B3,則由![]() 和弦B1B3圍成的弓形面積為 ;
和弦B1B3圍成的弓形面積為 ;
(3)線段CD,點C(6,4)、D(5,1),在⊙A上有一點M,使△CDM的面積最大,請找到此時的點M(保留必要輔助格點N).
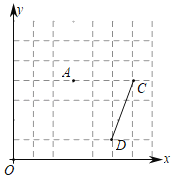
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式及其驗證過程:![]() ,驗證:
,驗證:![]() ,驗證:
,驗證:![]() .
.
(1)按照上述兩個等式及其驗證過程,猜想![]() 的變形結果并進行驗證;
的變形結果并進行驗證;
(2)針對上述各式反映的規律,直接寫出用a(a≥2的整數)表示的等式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在坐標系![]() 中,拋物線
中,拋物線![]() 經過點
經過點![]() 和
和![]() ,與
,與![]() 軸交于點
軸交于點![]() .直線
.直線![]() .
.
![]() 拋物線的解析式為 .直線
拋物線的解析式為 .直線![]() 的解析式為 ;
的解析式為 ;
![]() 若直線
若直線![]() 與拋物線只有一個公共點,求直線
與拋物線只有一個公共點,求直線![]() 的解析式;
的解析式;
![]() 設拋物線的頂點關于
設拋物線的頂點關于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() 是拋物線對稱軸上一動點,如果直線
是拋物線對稱軸上一動點,如果直線![]() 與拋物線在
與拋物線在![]() 軸上方的部分形成了封閉圖形(記為圖形
軸上方的部分形成了封閉圖形(記為圖形![]() ).請結合函數的圖象,直接寫出點
).請結合函數的圖象,直接寫出點![]() 的縱坐標
的縱坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com