
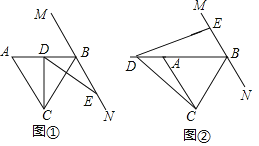
【題目】如圖,△ABC是等邊三角形,過點B作MN∥AC,D是射線BA上的動點,射線DC繞點D逆時針旋轉60°得射線DE,DE交MN于E.
(1)如圖①,當D為AB中點時,求證:BD+BE=BC;
(2)如圖②,當D在BA延長線上時,(1)的結論是否成立?若成立,請證明;若不成立,請寫出BC,BD,BE三條線段的數量關系,并說明理由;
(3)當∠DCA=15°時,直接寫出BD,BE的數量關系.
【答案】(1)見解析;(2)結論不成立.BD﹣BE=BC,見解析;(3)BD=(1+![]() )BE或BD=(
)BE或BD=(![]() +
+![]() )BE
)BE
【解析】
(1)如圖1中,連接EC.首先證明C,D,B,E四點共圓,推出△DCE是等邊三角形,再證明△ACD≌△BCE(SAS)可得結論.
(2)如圖2中,結論不成立.BD﹣BE=BC.證明方法類似(1),利用全等三角形的性質解決問題即可.
(3)分兩種情形:①如圖③﹣1中,當點D在線段AB上時,結論:BD=(1+![]() )BE.②如圖③﹣2中,當點D在BA的延長線上時,結論:BD=(
)BE.②如圖③﹣2中,當點D在BA的延長線上時,結論:BD=(![]() +
+![]() )BE,利用參數解直角三角形解決問題即可.
)BE,利用參數解直角三角形解決問題即可.
(1)證明:如圖1中,連接EC.

∵△ABC是等邊三角形,
∴CA=CB=AB,∠ACB=∠ABC=60°,
∵MN∥AC,
∴∠CBE=∠ACB=60°,
∵∠CDE=60°,
∴∠CDE=∠CBE=60°,
∴C,D,B,E四點共圓,
∴∠CED=∠CBD=60°,
∴△DCE是等邊三角形,
∴∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵BC=AB=AD+BD,
∴BC=BE+BD.
(2)解:如圖2中,結論不成立.BD﹣BE=BC.
理由:連接EC.
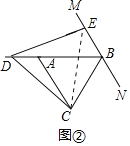
∵△ABC是等邊三角形,
∴CA=CB=AB,∠ACB=∠ABC=∠CAB=60°,
∵MN∥AC,
∴∠EBA=∠CAB=60°,
∴∠EBC=120°,
∵∠CDE=60°,
∴∠CDE+∠CBE=180°,
∴C,D,E,B四點共圓,
∴∠CED=∠CBD=60°,
∴△DCE是等邊三角形,
∴∠DCE=∠ACB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵BC=AB=BD﹣AD
∴BC=BD﹣BE.
(3)解:①如圖③﹣1中,當點D在線段AB上時,結論:BD=(1+![]() )BE.
)BE.
理由:作BH⊥DE于H,在DE上取一點K,使得DK=BK,連接BK.
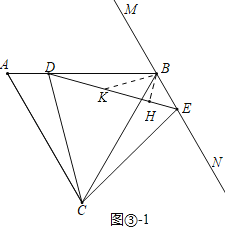
∵∠ACD=15°,∠A=∠CDE=60°,∠BDC=∠A+∠ACD,
∴∠BDE=∠ACD=60°,
∵MN∥AC,
∴∠CBN=∠ACB=60°,
∵∠ABC=60°,
∴∠DBE=120°,∠DEB=45°,
∵BH⊥DE,
∴∠BHE=∠BHD=90°,
∴∠HBE=∠HEB=45°,
∴BH=EH,設BH=EH=x,則BE=![]() =
=![]() x,
x,
∵DK=KB,
∴∠KDB=∠KBD=15°,
∴∠BKE=∠KDB+∠KBD=30°,
∴BK=DK=2x,KH=BKcos30°=![]() x,
x,
∴BD=![]() =
=![]() =(
=(![]() )x,
)x,
∴![]() =
=![]() =1+
=1+![]() ,
,
∴BD=(1+![]() )BE.
)BE.
②如圖③﹣2中,當點D在BA的延長線上時,結論:BD=(![]() +
+![]() )BE,
)BE,
理由:作EH⊥AB于H.
在DB上取一點G,使得DG=EG,連接EG.
設EH=m.
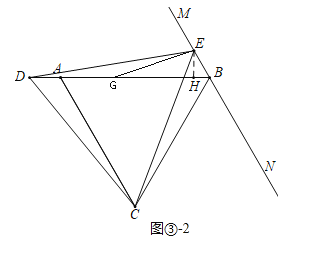
同法可證:∠EDB=15°,∠EBH=60°,
∴∠EGB=30°,
則有DH=DG+GH=EG+GH=EH÷sin30°+EH÷tan30°=2m+![]() m,EB=EH÷sin60°=
m,EB=EH÷sin60°=![]() m,
m,
∴![]() =
=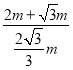 =
=![]() +
+![]()
∴BD=(![]() +
+![]() )BE,
)BE,


科目:初中數學 來源: 題型:
【題目】小亮一家在一湖泊中游玩,湖泊中有一孤島,媽媽在孤島P處觀看小亮與爸爸在湖中劃船(如圖所示).小船從P處出發,沿北偏東60°方向劃行200米到A處,接著向正南方向劃行一段時間到B處.在B處小亮觀測到媽媽所在的P處在北偏西37°的方向上,這時小亮與媽媽相距多少米(精確到1米)?
(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近日,國產航母山東艦成為了新晉網紅,作為我國本世紀建造的第一艘真正意義上的國產航母,承載了我們太多期盼,促使我國在偉大復興路上加速前行如圖,山東艦在一次測試中,巡航到海島A北偏東60°方向P處,發現在海島A正東方向有一可疑船只B正沿BA方向行駛。山東艦經測量得出:可疑船只在P處南偏東45°方向,距P處![]() 海里。山東艦立即從P沿南偏西30°方向駛出,剛好在C處成功攔截可疑船只。求被攔截時,可疑船只距海島A還有多少海里?(
海里。山東艦立即從P沿南偏西30°方向駛出,剛好在C處成功攔截可疑船只。求被攔截時,可疑船只距海島A還有多少海里?(![]() ,結果精確到0.1海里)
,結果精確到0.1海里)
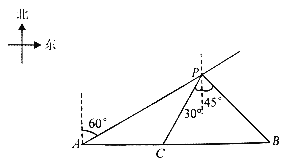
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在生活中,有很多函數并不一定存在解析式,對于這樣的函數,我們可以通過列表和圖象來對它可能存在的性質進行探索,例如下面這樣一個問題:
已知y是x的函數,下表是y與x的幾組對應值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孫同學根據學習函數的經驗,利用上述表格反映出的y與x之間的變化規律,對該函數的圖象與性質進行了探究.
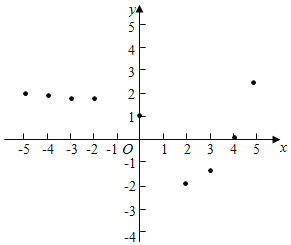
下面是小孫同學的探究過程,請補充完整;
(1)如圖,在平面之間坐標系xOy中,描出了以上表中各對應值為坐標的點,根據描出的點,畫出函數的圖象:
(2)根據畫出的函數圖象回答:
①x=﹣1時,對應的函數值y的為 ;
②若函數值y>0,則x的取值范圍是 ;
③寫出該函數的一條性質(不能與前面已有的重復): .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著社會經濟的發展,汽車逐漸走入平常百姓家.某數學興趣小組隨機抽取了我市某單位部分職工進行調查,對職工購車情況分4類(A:車價40萬元以上;B:車價在20﹣40萬元;C:車價在20萬元以下;D:暫時未購車)進行了統計,并將統計結果繪制成以下條形統計圖和扇形統計圖.請結合圖中信息解答下列問題:

(1)調查樣本人數為 ,樣本中B類人數百分比是 ,其所在扇形統計圖中的圓心角度數是 ;
(2)把條形統計圖補充完整;
(3)該單位甲、乙兩個科室中未購車人數分別為2人和3人,現從這5個人中選2人去參觀車展,用列表或畫樹狀圖的方法,求選出的2人來自不同科室的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某建筑物,從10m高的窗口A,用水管向外噴水,噴出的水呈拋物線狀(拋物線所在的平面與墻面垂直),如圖所示,如果拋物線的最高點M離墻1m,離地面![]() m,則水流落地點B離墻的距離OB是( )
m,則水流落地點B離墻的距離OB是( )
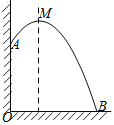
A.2mB.3mC.4mD.5m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大學生利用業余時間參與了一家網店經營,銷售一種成本為30元/件的文化衫,根據以往的銷售經驗,他整理出這種文化衫的售價y1(元/件),銷量y2(件)與第x(1≤x<90)天的函數圖象如圖所示(銷售利潤=(售價-成本)×銷量).
(1)求y1與y2的函數解析式.
(2)求每天的銷售利潤W與x的函數解析式.
(3)銷售這種文化衫的第多少天,銷售利潤最大,最大利潤是多少?


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,小剛家,菜地,稻田在同一條直線上.小剛從家去菜地澆水,又去稻田除草,然后回家.如圖反映了這個過程中,小剛離家的距離y與時間x之間的對應關系.如果菜地和稻田的距離為akm,小剛在稻田除草比在菜地澆水多用了bmin,則a,b的值分別為( )
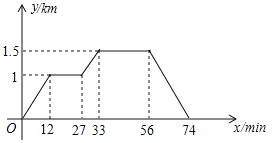
A.1,8B.0.5,12C.1,12D.0.5,8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com