
【題目】如圖,邊長為4的等邊三角形AOB的頂點O在坐標原點,點A在x軸的正半軸上,點B在第一象限.點P從點O出發,沿x軸以每秒1個單位長的速度向點A勻速運動,當點P到達點A時停止運動,設點P運動的時間是t秒.將線段BP的中點繞點P按順時針方向旋轉60°得點C,點C隨點P的運動而運動,連接CP、CA.過點P作PD⊥OB于D點
(1)直接寫出BD的長并求出點C的坐標(用含t的代數式表示)
(2)在點P從O向A運動的過程中,△PCA能否成為直角三角形?若能,求t的值.若不能,請說明理由;
(3)點P從點O運動到點A時,點C運動路線的長是多少?
【答案】
(1)解:∵△AOB是等邊三角形,
∴OB=OA=AB=4,∠BOA=∠OAB=∠ABO=60°.
∵PD⊥OB,
∴∠PDO=90°,
∴∠OPD=30°,
∴OD= ![]() OP.
OP.
∵OP=t,
∴OD= ![]() t,
t,
∴BD=4﹣ ![]() t.
t.
在Rt△OPD中,由勾股定理,得PD= ![]() t,
t,
如圖(1),過C作CE⊥OA于E,

則∠PEC=90°,
∵線段BP的中點繞點P按順時針方向旋轉60°得點C,
∴∠BPC=60°.
∵∠OPD=30°,
∴∠BPD+∠CPE=90°.
∴∠DBP=∠CPE
∴△PCE∽△BPD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴CE= ![]() ,PE=2﹣
,PE=2﹣ ![]() ,
,
∴OE=OP+PE=2+ ![]() ,
,
∴C(2+ ![]() ,
, ![]() )
)
(2)解:如圖(3),當∠PCA=90度時,作CF⊥PA,

∴△PCF∽△ACF,
∴ ![]() =
= ![]() ,
,
∴CF2=PFAF,
∵PF=2﹣ ![]() t,AF=4﹣OF=2﹣
t,AF=4﹣OF=2﹣ ![]() t,CF=
t,CF= ![]() t,
t,
∴( ![]() t)2=(2﹣
t)2=(2﹣ ![]() t)(2﹣
t)(2﹣ ![]() t),
t),
解得t=2,
此時P是OA的中點.
如圖(2),

當∠CAP=90°時,C的橫坐標就是4,
∴2+ ![]() t=4,
t=4,
解得t= ![]()
(3)解:設C(x,y),
∴x=2+ ![]() t,y=
t,y= ![]() t,
t,
∴y= ![]() x﹣
x﹣ ![]() ,
,
∴C點的運動痕跡是一條線段(0≤t≤4).
當t=0時,C1(2,0),
當t=4時,C2(5, ![]() ),
),
∴由兩點間的距離公式得:C1C2=2 ![]() .
.
故點C運動路線的長為:2 ![]()
【解析】(1)利用30度角的性質和旋轉性質、相似三角形性質,即△PCE∽△BPD,對應邊成比例可求出C坐標;(2)可先假設△PCA能成為直角三角形,分類討論,當∠PCA=90度時或∠CAP=90°,可利用相似性質列出對應邊成比例式子,進行求解;(3)可設出設C(x,y),構建參數方程x=2+ ![]() t,y=
t,y= ![]() t,消去參數即可得到y=
t,消去參數即可得到y= ![]() x﹣
x﹣ ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,AB∥OC,A(0,﹣4),B(a,b),C(c,0),并且a,c滿足c=![]() +10.一動點P從點A出發,在線段AB上以每秒2個單位長度的速度向點B運動;動點Q從點O出發在線段OC上以每秒1個單位長度的速度向點C運動,點P,Q分別從點A,O同時出發,當點P運動到點B時,點Q隨之停止運動,設運動時間為t(秒).
+10.一動點P從點A出發,在線段AB上以每秒2個單位長度的速度向點B運動;動點Q從點O出發在線段OC上以每秒1個單位長度的速度向點C運動,點P,Q分別從點A,O同時出發,當點P運動到點B時,點Q隨之停止運動,設運動時間為t(秒).
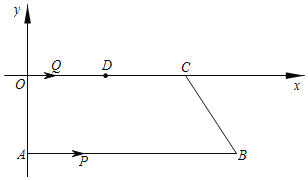
(1)求B,C兩點的坐標;
(2)當t為何值時,四邊形PQCB是平行四邊形?
(3)點D為線段OC的中點,當t為何值時,△OPD是等腰三角形?直接寫出t的所有值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點O為對角線AC的中點,過點o作射線OG、ON分別交AB,BC于點E,F,且∠EOF=90°,BO、EF交于點P.則下列結論中:
⑴圖形中全等的三角形只有兩對;
⑵正方形ABCD的面積等于四邊形OEBF面積的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正確的結論有( )個.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲船勻速順流而下從![]() 港到
港到![]() 港,同時乙船勻速逆流而上從
港,同時乙船勻速逆流而上從![]() 港到
港到![]() 港,
港,![]() 港處于
港處于![]() 、
、![]() 兩港的正中間,某個時刻,甲船接到通知需立即掉頭逆流而上到
兩港的正中間,某個時刻,甲船接到通知需立即掉頭逆流而上到![]() 處,到
處,到![]() 處后迅速按原順流速度駛向
處后迅速按原順流速度駛向![]() 港,最后甲、乙兩船都到達了各自的目的地.甲、乙兩船在靜水中的速度相同,設甲、乙兩船與
港,最后甲、乙兩船都到達了各自的目的地.甲、乙兩船在靜水中的速度相同,設甲、乙兩船與![]() 港的距離之和為
港的距離之和為![]() ,行駛時間為
,行駛時間為![]() ,
,![]() 與
與![]() 的部分關系如圖,則當兩船在
的部分關系如圖,則當兩船在![]() 、
、![]() 間某處相超時,兩船距離
間某處相超時,兩船距離![]() 港的距離為________千米.
港的距離為________千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,從點P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次擴展下去,則P2020的坐標為_____.
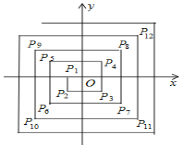
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個長5m的梯子AB,斜靠在一豎直的墻AO上,這時AO的距離為4m,如果梯子的頂端A沿墻下滑1m至C點.
(1)求梯子底端B外移距離BD的長度;
(2)猜想CE與BE的大小關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知⊙A經過點E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),則cos∠OBC的值為( )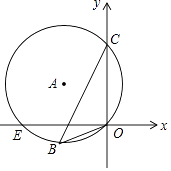
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:有一組對角相等而另一組對角不相等的凸四邊形叫做“湘一四邊形”.
(1)已知:如圖1,四邊形![]() 是“湘一四邊形”,
是“湘一四邊形”,![]() ,
,![]() ,
,![]() .則
.則![]() ,
, ![]() ,若
,若![]() ,
,![]() ,則
,則![]() (直接寫答案)
(直接寫答案)
(2)已知:在“湘一四邊形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .求對角線
.求對角線![]() 的長(請畫圖求解),
的長(請畫圖求解),
(3)如圖(2)所示,在四邊形![]() 中,若
中,若![]() ,當
,當![]() 時,此時四邊形
時,此時四邊形![]() 是否是“湘一四邊形”,若是,請說明理由:若不是,請進一步判斷它的形狀,并給出證明.
是否是“湘一四邊形”,若是,請說明理由:若不是,請進一步判斷它的形狀,并給出證明.
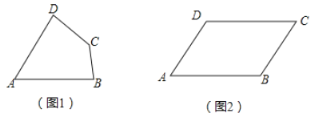
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市荸薺喜獲豐收,某生產基地收獲荸薺40噸.經市場調查,可采用批發、零售、加工銷售三種銷售方式,這三種銷售方式每噸荸薺的利潤如下表:
銷售方式 批發 零售 加工銷售
利潤(百元/噸) 12 22 30
設按計劃全部售出后的總利潤為y百元,其中批發量為x噸,且加工銷售量為15噸.
(1)求y與x之間的函數關系式;
(2)若零售量不超過批發量的4倍,求該生產基地按計劃全部售完荸薺后獲得的最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com