
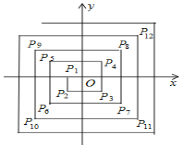
【題目】如圖,在平面直角坐標系中,從點P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次擴展下去,則P2020的坐標為_____.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
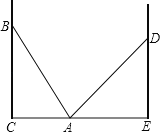
【題目】如圖,在兩面墻之間有一個底端在A點的梯子,當它靠在一側的墻上時,梯子的頂端在B點,當它靠在另一側的墻上時,梯子的頂端在D點,已知∠BAC=60°,點B到地面的垂直距離BC=5![]() 米,DE=6米.
米,DE=6米.
(1)求梯子的長度;
(2)求兩面墻之間的距離CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一矩形紙片OABC放在直角坐標系中,O為原點,C在x軸上,OA=6,OC=10.
(Ⅰ)如圖①,在OA上取一點E,將△EOC沿EC折疊,使點O落在AB邊上的D點,求E點的坐標;
(Ⅱ)如圖②,在OA、OC邊上選取適當的點E′、F,將△E′OF沿E′F折疊,使O點落在AB邊上D′點,過D′作D′G∥OA交E′F于T點,交OC于G點,設T的坐標為(x,y),求y與x之間的函數關系式,并直接寫出自變量x的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,若OG=2 ![]() ,求△D′TF的面積.(直接寫出結果即可)
,求△D′TF的面積.(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ACDE 是證明勾股定理時用到的一個圖形,a 、b 、c 是 RtABC和 RtBED 的邊長,已知![]() ,這時我們把關于 x 的形如
,這時我們把關于 x 的形如![]() 二次方程稱為“勾系一元二次方程”.
二次方程稱為“勾系一元二次方程”.

請解決下列問題:
(1)寫出一個“勾系一元二次方程”;
(2)求證:關于 x 的“勾系一元二次方程”![]() ,必有實數根;
,必有實數根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一個根,且四邊形 ACDE 的周長是6
的一個根,且四邊形 ACDE 的周長是6![]() ,求ABC 的面積.
,求ABC 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近日天氣晴朗,某集團公司準備組織全體員工外出踏青.決定租用甲、乙、丙三種型號的巴士出行,甲型巴士每輛車的乘載量是乙型巴士的3倍,丙型巴士每輛可乘坐36人.現在旅游公司有甲、乙、丙型巴士若干輛,預計給該集團公司安排申型、丙型巴士共計8輛,其余員工安排乙型巴士,每輛巴士均滿載,這樣乘坐乙型巴士和丙型巴士的員工共296人.臨行前,突然有若干人因特殊原因請假,這樣一來剛好可以減少租用一輛乙型包士,且有一輛乙型巴士多出兩個空位,這樣甲、乙兩種型號巴士共計裝載178人;則該集團公司共有________名員工.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為4的等邊三角形AOB的頂點O在坐標原點,點A在x軸的正半軸上,點B在第一象限.點P從點O出發,沿x軸以每秒1個單位長的速度向點A勻速運動,當點P到達點A時停止運動,設點P運動的時間是t秒.將線段BP的中點繞點P按順時針方向旋轉60°得點C,點C隨點P的運動而運動,連接CP、CA.過點P作PD⊥OB于D點
(1)直接寫出BD的長并求出點C的坐標(用含t的代數式表示)
(2)在點P從O向A運動的過程中,△PCA能否成為直角三角形?若能,求t的值.若不能,請說明理由;
(3)點P從點O運動到點A時,點C運動路線的長是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
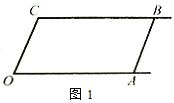
【題目】如圖1,已知射線CB∥OA,∠C=∠OAB,
(1)求證:AB∥OC;
(2)如圖2,E、F在CB上,且滿足∠FOB=∠AOB,OE平分∠COF.
①當∠C=110°時,求∠EOB的度數.
②若平行移動AB,那么∠OBC :∠OFC的值是否隨之發生變化?若變化,找出變
化規律;若不變,求出這個比值.
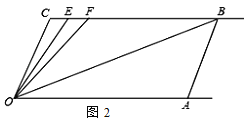
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是腰長為1的等腰直角三形,以Rt△ABC的斜邊AC為直角邊,畫第二個等腰Rt△ACD,再以Rt△ACD的斜邊AD為直角邊,畫第三個等腰Rt△ADE,…,依此類推,則第2018個等腰直角三角形的斜邊長是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五名同學在一次數學測驗中的平均成績是80分,而
五名同學在一次數學測驗中的平均成績是80分,而![]() ,
,![]() ,
,![]() 三人的平均成績是78分,下列說法一定正確的是( )
三人的平均成績是78分,下列說法一定正確的是( )
A.![]() ,
,![]() 兩人的平均成績是83分B.
兩人的平均成績是83分B.![]() ,
,![]() 的成績比其他三人都好
的成績比其他三人都好
C.五人成績的中位數一定是80分D.五人的成績的眾數一定是80分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com