
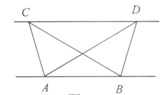
 中線,交BE于G.
中線,交BE于G. (1)證明:延長CD交BA延長線于H.
(1)證明:延長CD交BA延長線于H.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 26、探究題.
26、探究題.查看答案和解析>>
科目:初中數學 來源: 題型:
 13、探究題:
13、探究題:查看答案和解析>>
科目:初中數學 來源: 題型:
 的圖象上,過點M作ME⊥y軸,過點N作NF⊥x軸,垂足分別為E,F.證明:MN∥EF.
的圖象上,過點M作ME⊥y軸,過點N作NF⊥x軸,垂足分別為E,F.證明:MN∥EF.
 的圖象上,且M(2,m),N是第三象限內反比例函數y=
的圖象上,且M(2,m),N是第三象限內反比例函數y= 的圖象上一動點.過點M作ME⊥y軸,過點N作EF⊥x軸,垂足分別為E,F.說明MN∥EF.并求當四邊形MEFN的面積為12時點N的坐標.
的圖象上一動點.過點M作ME⊥y軸,過點N作EF⊥x軸,垂足分別為E,F.說明MN∥EF.并求當四邊形MEFN的面積為12時點N的坐標.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com