
【題目】(1)探究:如圖①,直線AB、BC、AC兩兩相交,交點分別為點A、B、C,點D在線段AB上,過點D作DE∥BC交AC于點E,過點E作EF∥AB交BC于點F.若∠ABC=40°,求∠DEF的度數.
請將下面的解答過程補充完整,并填空(理由或數學式)
解:∵DE∥BC,∴∠DEF= .( )
∵EF∥AB,∴ =∠ABC.( )
∴∠DEF=∠ABC.(等量代換)
∵∠ABC=40°,∴∠DEF= °.
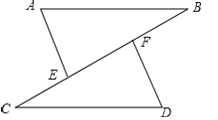
(2)應用:如圖②,直線AB、BC、AC兩兩相交,交點分別為點A、B、C,點D在線段AB的延長線上,過點D作DE∥BC交AC于點E,過點E作EF∥AB交BC于點F.若∠ABC=60°,則∠DEF= °.

【答案】(1)答案見解析;(2)120.
【解析】試題分析:(1)依據兩直線平行,內錯角相等;兩直線平行,同位角相,即可得到∠DEF=40°.
(2)依據兩直線平行,內同位角相;兩直線平行,同旁內角互補,即可得到∠DEF=180°-60°=120°.
試題解析:(1)∵DE∥BC,
∴∠DEF=∠EFC.(兩直線平行,內錯角相等)
∵EF∥AB,
∴∠EFC=∠ABC.(兩直線平行,同位角相等)
∴∠DEF=∠ABC.(等量代換)
∵∠ABC=40°,
∴∠DEF=40°.
故答案為:∠EFC,兩直線平行,內錯角相等,∠EFC,兩直線平行,同位角相等,40;

(2)∵DE∥BC,
∴∠ABC=∠EADE=60°.(兩直線平行,內同位角相等)
∵EF∥AB,
∴∠ADE+∠DEF=180°.(兩直線平行,同旁內角互補)
∴∠DEF=180°-60°=120°.
故答案為:120.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB、DC被BD所截得的內錯角是___________,AB、CD被AC所截是的內錯角是_________,AD、BC被BD所截得的內錯角是_________,AD、BC被AC所截得的內錯角是_____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C,E,F,B在同一直線上,點A,D在BC異側,AB∥CD,AE=DF,∠A=∠D.
(1)求證:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的對角線AC、BD相交于點O,∠BAC的平分線交BD于點E,交BC于點F,點G是AD的中點,連接CG交BD于點H,連接FO并延長FO交CG于點P,則PG:PC的值為 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別相交于點A,B,四邊形ABCD是正方形,拋物線
軸分別相交于點A,B,四邊形ABCD是正方形,拋物線![]() 在經過A,D兩點.
在經過A,D兩點.

(1)求該拋物線表達式;
(2)連接BD,將線段BD繞著D點順時針旋轉90度,得到DB’.直接寫出點B’的坐標,并判斷點B’是否落在拋物線上,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 下列事件中,最適合采用全面調查的是( )
A.對某班全體學生出生日期的調查B.對全國中小學生節水意識的調查
C.對某批次的燈泡使用壽命的調查.D.對廈門市初中學生每天閱讀時間的調查
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于某一函數,給出如下定義:若存在實數![]() ,對于一函數任意的函數值
,對于一函數任意的函數值![]() ,函數值都滿足
,函數值都滿足![]() ,則稱這個函數是有界函數,同時進一步規定,對某個有界函數,在所有滿足條件的
,則稱這個函數是有界函數,同時進一步規定,對某個有界函數,在所有滿足條件的![]() 中,其最小值稱為這個有界函數的確界值.例如如圖所示的函數是有界函數,其確界值是1.5.
中,其最小值稱為這個有界函數的確界值.例如如圖所示的函數是有界函數,其確界值是1.5.
問:將有界函數![]() +
+![]()
![]() 的圖象向上平移
的圖象向上平移![]() 個單位,得到的新函數的確界值是
個單位,得到的新函數的確界值是![]() ,當
,當![]() 在什么范圍時,滿足
在什么范圍時,滿足![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com