
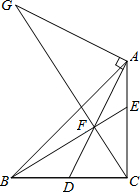
 如圖,Rt△ABC中,∠BCA=90°,AC=BC,點D是BC的中點,點F在線段AD上,DF=CD,BF交CA于E點,過點A作DA的垂線交CF的延長線于點G,下列結論:①CF2=EF•BF;②AG=2DC;③AE=EF;④AF•EC=EF•EB.其中正確的結論有①②④.
如圖,Rt△ABC中,∠BCA=90°,AC=BC,點D是BC的中點,點F在線段AD上,DF=CD,BF交CA于E點,過點A作DA的垂線交CF的延長線于點G,下列結論:①CF2=EF•BF;②AG=2DC;③AE=EF;④AF•EC=EF•EB.其中正確的結論有①②④. 分析 根據等邊對等角的性質求出∠DCF=∠DFC,然后求出DF=DB,根據等邊對等角求出∠DBF=∠DFB,然后求出∠BFC是直角,根據直角三角形的性質求出△BCF和△CEF相似,根據相似三角形對應邊成比例列式整理即可得到①正確;根據互余關系求出∠G=∠ACG,再根據等角對等邊的性質求出AG=AC,然后求出AG=BC,然后利用“角角邊”證明△BCE和△AGF全等,根據全等三角形對應邊相等可得AG=BC,從而判斷②正確;根據角的互余關系可以求出∠EAF+∠ADC=90°,∠AFE+∠DFC=90°再根據∠ADC的正切值為2可知∠ADC≠60°,然后求出∠FDC≠∠DFC,然后求出∠EAF≠∠EFA,從而得到AE≠EF,判斷出③錯誤;根據根據直角三角形的性質求出△CEF和△BCE相似,根據相似三角形的對應邊成比例列式求出EC2=EF•EB,再根據全等三角形對應邊相等可得AF=CE,從而判斷出④正確.
解答 解:∵DF=CD,
∴∠DCF=∠DFC,
∵AC=BC,點D是BC的中點,
∴DF=DB=DC,
∴∠DBF=∠DFB,
又∵∠DBF+∠DFB+∠DFC+∠DCF=180°,
∴∠BFC=$\frac{1}{2}$×180°=90°,
∴CF⊥BE,
∴Rt△BCF∽Rt△CEF,
∴$\frac{CF}{EF}$=$\frac{BF}{CF}$,
∴CF2=EF•BF,故①正確;
∵AG⊥AD,
∴∠G+∠AFG=90°,
又∵∠ACG+∠DCF=90°,∠DCF=∠DFC=∠AFG,
∴∠G=∠ACG,
∴AG=AC,
∵AC=BC,
∴AG=BC,
又∵∠CBE=∠ACG,
∴∠CBE=∠G,
在△BCE和△AGF中,
∵$\left\{\begin{array}{l}{∠GAF=∠BCE=90°}\\{∠CBE=∠G}\\{AG=BC}\end{array}\right.$,
∴△BCE≌△AGF(AAS),
∴AG=BC,
∵點D是BC的中點,
∴BC=2DC,
∴AG=2DC,故②正確;
根據角的互余關系,∠EAF+∠ADC=90°,∠AFE+∠DFC=90°,
∵tan∠ADC=2,
∴∠ADC≠60°,
∵∠DCF=∠DFC,
∴∠FDC≠∠DFC,
∴∠EAF≠∠EFA,
∴AE≠EF,故③錯誤;
∵∠ACB=90°,CF⊥BE,
∴△CEF∽△BCE,
∴$\frac{EC}{EB}$=$\frac{EF}{EC}$,
∴EC2=EF•EB,
∵△BCE≌△AGF(已證),
∴AF=EC,
∴AF•EC=EF•EB,故④正確;
所以,正確的結論有①②④.
故答案為①②④.
點評 本題考查了相似三角形的判定與性質,全等三角形的判定與性質,等腰直角三角形的性質,根據等角對等邊以及等邊對等角的性質求出AG=AC,然后證明△BCE和△AGF全等是證明的關鍵,也是本題的難點.


科目:初中數學 來源: 題型:選擇題

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=2x | B. | y=${x^2}+\frac{1}{x}$ | C. | y=$\sqrt{{x}^{2}-2x+1}$ | D. | y=x2-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
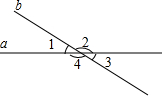 如圖,已知直線a、b相交,∠1=40°,求∠2、∠3、∠4的度數
如圖,已知直線a、b相交,∠1=40°,求∠2、∠3、∠4的度數查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com