
【題目】按圖填空,并注明理由. 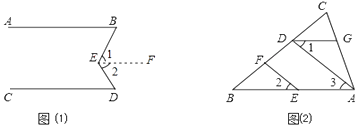
(1)完成正確的證明:如圖(1),已知AB∥CD,求證:∠BED=∠B+∠D
證明:過E點作EF∥AB(經過直線外一點有且只有一條直線與這條直線平行)
∴∠1=()
∵AB∥CD(已知)
∴EF∥CD(如果兩條直線與同一直線平行,那么它們也平行)
∴∠2=()
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代換).
(2)如圖(2),在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.將求∠AGD的過程填寫完整.
解:因為EF∥AD(已知)
所以∠2=∠3.()
又因為∠1=∠2,所以∠1=∠3.(等量代換)
所以AB∥()
所以∠BAC+=180° ().
又因為∠BAC=70°,所以∠AGD=110°.
【答案】
(1)∠B;兩直線平行,內錯角相等;∠D;兩直線平行,內錯角相等
(2)兩直線平行,同位相等;DG;內錯角相等,兩直線平行;∠AGD;兩直線平行,同旁內角互補
【解析】(1)證明:過E點作EF∥AB(經過直線外一點有且只有一條直線與這條直線平行)
∴∠1=∠B(兩直線平行,同位相等)
∵AB∥CD(已知)
∴EF∥CD(如果兩條直線與同一直線平行,那么它們也平行)
∴∠2=∠D(內錯角相等,兩直線平行)
又∠BED=∠1+∠2,
∴∠BED=∠B+∠D (等量代換).
·(2)解:因為EF∥AD(已知)
所以∠2=∠3.(兩直線平行,同位相等)
又因為∠1=∠2,所以∠1=∠3.(等量代換)
所以AB∥DG(內錯角相等,兩直線平行)
所以∠BAC+∠AGD=180° (兩直線平行,同旁內角互補).
又因為∠BAC=70°,所以∠AGD=110°
所以答案是:(1)∠B,兩直線平行,內錯角相等;∠D,兩直線平行,內錯角相等;兩直線平行,同位角相等;(2)DG,內錯角相等,兩直線平行;∠AGD,兩直線平行,同旁內角互補.
【考點精析】本題主要考查了平行公理和平行線的判定與性質的相關知識點,需要掌握平行公理――平行線的存在性與惟一性;經過直線外一點,有且只有一條直線與這條直線平行;如果兩條直線都與第三條直線平行,那么這兩條直線也互相平行;由角的相等或互補(數量關系)的條件,得到兩條直線平行(位置關系)這是平行線的判定;由平行線(位置關系)得到有關角相等或互補(數量關系)的結論是平行線的性質才能正確解答此題.


 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:
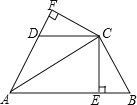
【題目】(本題8分) 已知,如圖,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求證:BE=DF;
(2)若AB=5,AD=3,求AE的長;
(3)若△ABC的面積是23,△ADC面積是18,則△BEC的面積等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若點A(2,4)在函數y=kx﹣2的圖象上,則下列各點在此函數圖象上的是( )
A. (1,1) B. (﹣1,1) C. (﹣2,﹣2) D. (2,﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算與化簡
(1)﹣7+13﹣6+20
(2)23×(﹣5)﹣(﹣3)÷ ![]()
(3)[﹣22﹣(5﹣6)3]÷ ![]() ×
× ![]() ﹣|﹣2|
﹣|﹣2|
(4)﹣(2y﹣5)+(4+3y)
(5)(8xy﹣x2+y2)﹣3(﹣x2+y2+5xy)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是“東方之星”救援打撈現場圖,小紅據此構造出一個如圖2所示的數學模型,已知:A、B、D三點在同一水平線上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.
(1)求點B到AC的距離;
(2)求線段CD的長度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com