
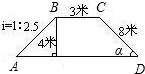
 如圖,攔水壩的橫斷面為梯形ABCD,根據圖示數據求:
如圖,攔水壩的橫斷面為梯形ABCD,根據圖示數據求: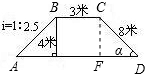 解:(1)過點C作CF⊥AD于F,則CF為梯形的高,
解:(1)過點C作CF⊥AD于F,則CF為梯形的高,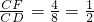 ,
, =
= ,
, =0.4,而tan∠A=
=0.4,而tan∠A=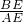 ,
,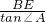 =
=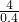 =10;
=10; =13+4
=13+4 ,
,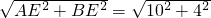 =
=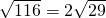 ,
, )米,斜坡AB=2
)米,斜坡AB=2 米.
米.

科目:初中數學 來源: 題型:
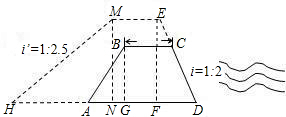 如圖,攔水壩的橫斷面為梯形ABCD,壩頂寬BC=6米,壩高3.2米,為了提高水壩的攔水能力,需將水壩加高2米,并且保持壩頂寬度不變,迎水坡CD的坡度不變,但是背水坡的坡度由原來的i=1:2變成i′=1:2.5(有關數據在圖上已注明),求加高后的壩底HD的長為多少?
如圖,攔水壩的橫斷面為梯形ABCD,壩頂寬BC=6米,壩高3.2米,為了提高水壩的攔水能力,需將水壩加高2米,并且保持壩頂寬度不變,迎水坡CD的坡度不變,但是背水坡的坡度由原來的i=1:2變成i′=1:2.5(有關數據在圖上已注明),求加高后的壩底HD的長為多少?查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
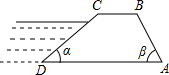 坡度為1:1,壩高為4米,求:
坡度為1:1,壩高為4米,求:查看答案和解析>>
科目:初中數學 來源: 題型:
 坡AB的坡度i=1:3(指坡面的鉛直高度AE與水平寬度BE的比),斜坡DC的坡度i=1:1.5,已知該攔水壩的高為6米.
坡AB的坡度i=1:3(指坡面的鉛直高度AE與水平寬度BE的比),斜坡DC的坡度i=1:1.5,已知該攔水壩的高為6米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com