
【題目】【操作發現】
如圖①,在邊長為1個單位長度的小正方形組成的網格中,△ABC的三個頂點均在格點上.

(1)請按要求畫圖:將△ABC繞點A按順時針方向旋轉90°,點B的對應點為B′,點C的對應點為C′,連接BB′;
(2)在(1)所畫圖形中,∠AB′B= .
【問題解決】
如圖②,在等邊三角形ABC中,AC=7,點P在△ABC內,且∠APC=90°,∠BPC=120°,求△APC的面積.
小明同學通過觀察、分析、思考,對上述問題形成了如下想法:
想法一:將△APC繞點A按順時針方向旋轉60°,得到△AP′B,連接PP′,尋找PA,PB,PC三條線段之間的數量關系;
想法二:將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,連接PP′,尋找PA,PB,PC三條線段之間的數量關系.
…
請參考小明同學的想法,完成該問題的解答過程.(一種方法即可)
【靈活運用】
如圖③,在四邊形ABCD中,AE⊥BC,垂足為E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k為常數),求BD的長(用含k的式子表示).
【答案】【操作發現】(1)作圖見解析;(2)45°;【問題解決】7![]() ;【靈活運用】
;【靈活運用】![]() .
.
【解析】試題分析:【操作發現】(1)根據旋轉角,旋轉方向畫出圖形即可;(2)只要證明△ABB′是等腰直角三角形即可;【問題解決】如圖②,將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,只要證明∠PP′C=90°,利用勾股定理即可解決問題;【靈活運用】如圖③中,由AE⊥BC,BE=EC,推出AB=AC,將△ABD繞點A逆時針旋轉得到△ACG,連接DG.則BD=CG,只要證明∠GDC=90°,可得CG=![]() ,由此即可解決問題.
,由此即可解決問題.
試題解析:【操作發現】(1)如圖所示,△AB′C′即為所求;

(2)連接BB′,將△ABC繞點A按順時針方向旋轉90°,
∴AB=AB′,∠B′AB=90°,
∴∠AB′B=45°,
故答案為:45°;
【問題解決】如圖②,

∵將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,
∴△APP′是等邊三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=![]() PC,即AP=
PC,即AP=![]() PC,
PC,
∵∠APC=90°,
∴AP2+PC2=AC2,即(![]() PC)2+PC2=72,
PC)2+PC2=72,
∴PC=2![]() ,
,
∴AP=![]() ,
,
∴S△APC=![]() APPC=7
APPC=7![]() ;
;
【靈活運用】如圖③中,∵AE⊥BC,BE=EC,
∴AB=AC,將△ABD繞點A逆時針旋轉得到△ACG,連接DG.則BD=CG,

∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=4k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() =
=![]() .
.
∴BD=CG=![]() .
.


科目:初中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 在數軸上分別表示有理數
在數軸上分別表示有理數![]() ,
,![]() .
.

(1)對照數軸填寫下表:
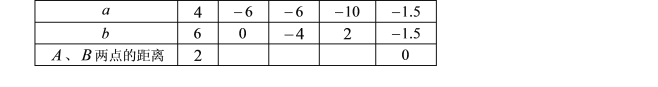
(2)若![]() ,
,![]() 兩點間的距離記為
兩點間的距離記為![]() ,試問
,試問![]() 和
和![]() ,
,![]() 有何數量關系;
有何數量關系;
(3)寫出數軸上到![]() 和
和![]() 的距離之和為
的距離之和為![]() 的所有整數;
的所有整數;
(4)若![]() 表示一個有理數,求
表示一個有理數,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,∠ABD、∠CDB的平分線BE、DF分別交邊AD、BC于點E、F.
(1)求證:四邊形BEDF是平行四邊形;
(2)當∠ABE為多少度時,四邊形BEDF是菱形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,我國很多地區持續出現霧霾天氣.某社區為了調查本社區居民對霧霾天氣主要成因的認識情況,隨機對該社區部分居民進行了問卷調查,要求居民從五個主要成因中只選擇其中的一項,被調查居民都按要求填寫了問卷.社區對調查結果進行了整理,繪制了如下不完整的統計圖表.被調查居民選擇各選項人數統計表
霧霾天氣的主要成因 | 頻數(人數) |
A大氣氣壓低,空氣不流動 | m |
B地面灰塵大,空氣濕度低 | 40 |
C汽車尾氣排放 | n |
D工廠造成的污染 | 120 |
E其他 | 60 |
請根據圖表中提供的信息解答下列問題:
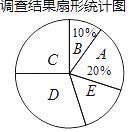
(1)填空:m=________,n=________,扇形統計圖中C選項所占的百分比為________.
(2)若該社區居民約有6 000人,請估計其中會選擇D選項的居民人數.
(3)對于“霧霾”這個環境問題,請你用簡短的語言發出倡議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,點M、N分別在AD、BC邊上,將矩形ABCD沿MN翻折,點C恰好落在AD邊上的點F處,若MD=1,∠MNC=60°,則AB的長為_____.
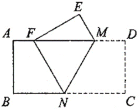
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于數軸上的A、B、C三點,給出如下定義:若其中一個點與其它兩個點的距離恰好滿足2倍的數量關系,則稱該點是其它兩個點的“至善點”.例如:若數軸上點A、B、C所表示的數分別為1、3、4,則點B是點A、C的“至善點”.
(1)若點A表示數﹣2,點B表示數2,下列各數![]() 、0、1、6所對應的點分別為C1、C2、C3、C4,其中是點A、B的“至善點”的有 (填代號);
、0、1、6所對應的點分別為C1、C2、C3、C4,其中是點A、B的“至善點”的有 (填代號);
(2)已知點A表示數﹣1,點B表示數3,點M為數軸上一個動點:
①若點M在點A的左側,且點M是點A、B的“至善點”,求此時點M表示的數m;
②若點M在點B的右側,點M、A、B中,有一個點恰好是其它兩個點的“至善點”,求出此時點M表示的數m.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中,二次函數y=x2﹣2mx+m2+2m+2的圖象與x軸有兩個交點.
(1)當m=﹣2時,求二次函數的圖象與x軸交點的坐標;
(2)過點P(0,m﹣1)作直線1⊥y軸,二次函數圖象的頂點A在直線l與x軸之間(不包含點A在直線l上),求m的范圍;
(3)在(2)的條件下,設二次函數圖象的對稱軸與直線l相交于點B,求△ABO的面積最大時m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,∠BAC的平分線AD交BC于點D,DE垂直平分AC,垂足為點E.
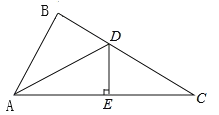
(1)證明∠BAD=∠C;
(2)∠BAD=29°,求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,點E在DC上,且AE,BE分別平分∠BAD和∠ABC.
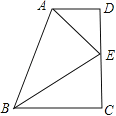
(1)求證:點E為CD中點;
(2)當AD=2,BC=3時,求AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com