
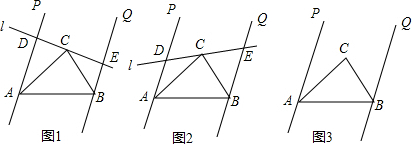
分析 (1)根據各線段之間的長度,先猜想AD+BE=AB;
(2)在AB上截取AG=AD,連接CG,利用三角形全等的判定定理可判斷出AD=AG.同理可證BG=BE,即AD+BE=AB;
(3)畫出直線l與直線MA不垂直且交點D、E在AB的異側時的圖形,分兩種情況討論:①當點D在射線AM上、點E在射線BN的反向延長線上時;②點D在射線AM的反向延長線上,點E在射線BN上時;得到AD,BE,AB之間的關系.
解答 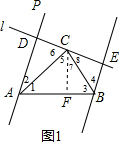 (1)證明:如圖1,過C作CF⊥AB于F,
(1)證明:如圖1,過C作CF⊥AB于F,
∵AC平分∠PAB,BC平分∠QBA
,∴∠1=∠2,∠3=∠4,
∵l⊥AP,PA∥BQ,
∴∠EDA=∠DEB=90°,
∴∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,
∴∠ACB=90°,
在△CDA與△CFA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠ADC=∠CFA=90°}\\{AC=AC}\end{array}\right.$,
∴△ACD≌△ACF,
∴AD=AF,
同理BF=BE,
∵AB=AF+BF,
∴AB=AD+BE;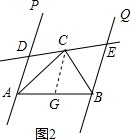 (2)如圖2,在AB上截取AG=AD,連接CG.
(2)如圖2,在AB上截取AG=AD,連接CG.
∵AC平分∠MAB,
∴∠DAC=∠CAB,
在△ADC與△AGC中,
$\left\{\begin{array}{l}{AD=AG}\\{∠DAC=∠GAC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△AGC(SAS),
∴∠DCA=∠ACG,
∵AP∥BQ,
∴∠DAC+∠CAB+∠GBC+∠CBE=180°,
∵∠DAC=∠CAB,∠GBC=∠CBE,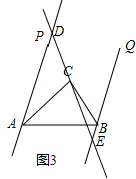 ∴∠CAB+∠GBC=90°,
∴∠CAB+∠GBC=90°,
∴∠ACB=90°即∠ACG+∠GCB=90°,
∵∠DCA+∠ACG+∠GCB+∠BCE=180°,
∴∠DCA+∠BCE=90°,
∴∠GCB=∠ECB,
在△BGC與△BEC中,
$\left\{\begin{array}{l}{∠GCB=∠ECB}\\{BC=BC}\\{∠ABC=∠CBE}\end{array}\right.$,
∴△BGC≌△BEC,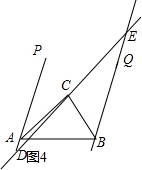 ∴BG=BE,
∴BG=BE,
∴AD+BE=AG+BG,
∴AD+BE=AB;
(3)不成立.
存在,當點D在射線AP上、點E在射線BN的反向延長線上時(如圖3),AD-BE=AB;
當點D在射線AP的反向延長線上,點E在射線BN上時(如圖4),BE-AD=AB.
點評 本題考查了全等三角形的判定和性質,平行線的性質,角平分線的定義,正確的作出輔助線是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,把△ABC繞點C按順時針方向旋轉35°,得到△A′B′C,A′B′交AC于點D.若
如圖,把△ABC繞點C按順時針方向旋轉35°,得到△A′B′C,A′B′交AC于點D.若| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
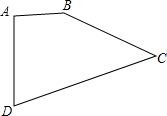 如圖,已知四邊形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四邊形ABCD的面積.
如圖,已知四邊形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四邊形ABCD的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com