
【題目】已知直線![]() 交
交![]() 軸于
軸于![]() 點,交
點,交![]() 軸于
軸于![]() 點,
點, ![]() 為
為![]() 的中點,
的中點, ![]() 為射線
為射線![]() 上一點,連
上一點,連![]() ,將
,將![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() 得線段
得線段![]() ,則
,則![]() 的最小值為__________.
的最小值為__________.
【答案】![]()
【解析】根據題意,畫出圖形(如圖所示),直線![]() 交
交![]() 軸于
軸于![]() 點,交
點,交![]() 軸于
軸于![]() 點,
點, ![]() 為
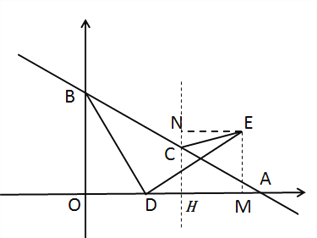
為![]() 的 中點,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.過點E作EM⊥x軸于點M,過點E作NC⊥x軸,過點E作EN⊥NC于點N,因為BD⊥DE,∠BOD=∠AMD=90°,即可證得∠ODB=∠MED,再由BD=DE,根據AAS即可判定△ODB≌△MED,根據全等三角形的對應邊相等可得OD=EM,OB=DM=2,設OD=EM=m,則OM=2+m,由點C為AB的中點可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根據勾股定理可得
的 中點,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.過點E作EM⊥x軸于點M,過點E作NC⊥x軸,過點E作EN⊥NC于點N,因為BD⊥DE,∠BOD=∠AMD=90°,即可證得∠ODB=∠MED,再由BD=DE,根據AAS即可判定△ODB≌△MED,根據全等三角形的對應邊相等可得OD=EM,OB=DM=2,設OD=EM=m,則OM=2+m,由點C為AB的中點可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根據勾股定理可得![]() ,當
,當![]() 時,
時, ![]() 最小,最小為
最小,最小為![]() ,所以EC最小為
,所以EC最小為![]() .
.


科目:初中數學 來源: 題型:
【題目】目前節能燈在城市已基本普及,為響應號召,某商場計劃購進甲,乙兩種節能燈共200只,這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲型 | 20 | 30 |
乙型 | 30 | 45 |
(1)若購進甲,乙兩種節能燈共用去5200元,求甲、乙兩種節能燈各進多少只?
(2)若商場準備用不多于5400元購進這兩種節能燈,問甲型號的節能燈至少進多少只?
(3)在(2)的條件下,該商場銷售完200只節能燈后能否實現盈利超過2690元的目標?若能請你給出相應的采購方案;若不能說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)先化簡,再求值:3x2﹣(2x2﹣xy+y2)+(﹣x2+3xy+2y2),其中x=﹣2,y=3.
(2)一個角比它的余角大20°,求這個角的補角度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與直線
與直線![]() 垂直相交于
垂直相交于![]() ,點
,點![]() 在射線
在射線![]() 上運動,點
上運動,點![]() 在射線
在射線![]() 上運動,連接
上運動,連接![]() .
.

(1)如圖1,已知![]() ,
,![]() 分別是
分別是![]() 和
和![]() 角的平分線,
角的平分線,
①點![]() ,
,![]() 在運動的過程中,
在運動的過程中,![]() 的大小是否發生變化?若發生變化,請說明理由;若不發生變化,試求出
的大小是否發生變化?若發生變化,請說明理由;若不發生變化,試求出![]() 的大小.
的大小.
②如圖2,將![]() 沿直線
沿直線![]() 折疊,若點
折疊,若點![]() 落在直線
落在直線![]() 上,記作點
上,記作點![]() ,則
,則![]() _______
_______![]() ;如圖3,將
;如圖3,將![]() 沿直線
沿直線![]() 折疊,若點
折疊,若點![]() 落在直線
落在直線![]() 上,記作點
上,記作點![]() ,則
,則![]() ________
________![]() .
.
(2)如圖4,延長![]() 至
至![]() ,已知
,已知![]() ,
,![]() 的角平分線與
的角平分線與![]() 的角平分線交其延長線交于
的角平分線交其延長線交于![]() ,
,![]() ,在
,在![]() 中,如果有一個角是另一個角的
中,如果有一個角是另一個角的![]() 倍,求
倍,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育課上,七年級某班男同學進行了100米測驗,達標成績為15秒,下表是夢想小組8名男生的成績記錄,其中“+”表示成績大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
問:(1)這個小組男生的達標率為多少?(達標率=![]() )
)
(2)這個小組男生的平均成績是多少秒?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 1,一張△ABC 紙片,點 M、N 分別是 AC、BC 上兩點.
(1)若沿直線 MN 折疊,使 C 點落在 BN 上,則∠AMC′與∠ACB 的數量關系是 ;

(2)若折成圖 2 的形狀.猜想∠AMC′、∠BNC′和∠ACB 的數量關系,并說明理由.
猜想: .
理由:
(3)若折成圖3 的形狀,猜想∠AMC′、∠BNC′和∠ACB 的數量關系是 .(寫出結論即可).
(4)將上述問題推廣,如圖4,將四邊形 ABCD 紙片沿 MN 折疊,使點 C、D 落在四邊形 ABNM 的內部時,∠AMD′+∠BNC′與∠C、∠D 之間的數量關系 是 (寫出結論即可).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品現在售價為每件60元,每星期可賣出300件,市場調查反映:調整價格,每件漲價1元,每星期要少賣出10件;每件降價1元,每星期可多賣出20件.已知商品的進價為每件40元.
(1)設每件降價x元,每星期的銷售利潤為y元;
① 請寫出y與x之間的函數關系式;
② 確定x的值,使利潤最大,并求出最大利潤;
(2)若漲價x元,則x= 元時,利潤y的最大值為 元(直接寫出答案,不必寫過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a≠0)圖象的一部分,對稱軸是直線x=-2.關于下列結論:①ab<0;②b2-4ac>0;③25a-5b+c>0;④b-4a=0;⑤方程ax2+bx=0的兩個根為x1=0,x2=-4,其中正確的結論有( )
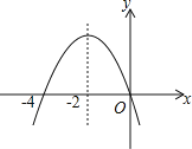
A. 2個 B. 3個
C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李明準備進行如下操作實驗,把一根長40 cm的鐵絲剪成兩段,并把每段首尾相連各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于58 cm2,李明應該怎么剪這根鐵絲?
(2)李明認為這兩個正方形的面積之和不可能等于48 cm2,你認為他的說法正確嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com