
如圖所示,在△ABC中,D、G分別是AB、AC上的點,且BD=CG,M、N分別是BG、CD的中點,過MN的直線交AB于P,交AC于Q.

求證:AP=AQ.
|
證明:取 BC的中點E,連ME,NE.在△GBC中,∵EM是中位線,∴EM解析:要證明 AP=AQ,只要證明∠APQ=∠AQP,為利用已知條件BD=CG及M、N為BG、CD的中點,故可考慮添加中位線為輔助線,即取BC邊的中點E,連EM、EN,則EM、EN分別是△BCG和△BCD的中位線.由中位線定理可得EM思維延伸:當已知條件中有中點的條件時,可考慮構造三角形的中位線,利用中位線的性質解決相關的問題. |


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
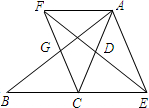 如圖所示,在△ABC中,D是AC的中點,E是線段BC延長線上一點,過點A作AF∥BC交ED的延長線于點F,連接AE,CF.
如圖所示,在△ABC中,D是AC的中點,E是線段BC延長線上一點,過點A作AF∥BC交ED的延長線于點F,連接AE,CF.查看答案和解析>>
科目:初中數學 來源: 題型:
 15、如圖所示,在△ABC中,DM、EN分別垂直平分AB和AC,交BC于D、E,若∠DAE=50°,則∠BAC=
15、如圖所示,在△ABC中,DM、EN分別垂直平分AB和AC,交BC于D、E,若∠DAE=50°,則∠BAC=查看答案和解析>>
科目:初中數學 來源: 題型:
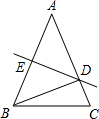 如圖所示,在△ABC中,AB=AC,DE是邊AB的垂直平分線,交AB于E,交AC于D,若△BCD的周長為18cm,△ABC的周長為30cm,那么BE的長為
如圖所示,在△ABC中,AB=AC,DE是邊AB的垂直平分線,交AB于E,交AC于D,若△BCD的周長為18cm,△ABC的周長為30cm,那么BE的長為查看答案和解析>>
科目:初中數學 來源: 題型:
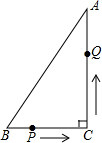 如圖所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P點在BC上從B點向C點運動(不包括點C),點P的運動速度為2cm∕s;Q點在AC上從C點向點A運動(不包括點A),運動速度為5cm∕s,若點P、Q分別從B、C同時運動,請解答下面的問題,并寫出主要過程.
如圖所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P點在BC上從B點向C點運動(不包括點C),點P的運動速度為2cm∕s;Q點在AC上從C點向點A運動(不包括點A),運動速度為5cm∕s,若點P、Q分別從B、C同時運動,請解答下面的問題,并寫出主要過程.| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com