解:(1)如圖,設正方形的邊長為a,
∵正方形的對邊MN∥PQ,
∴△AMN∽△ABC,
∴

=

,
即

=

,
解得a=12,
∴這個正方形的面積=a
2=12
2=144;

(2)當PQ在BC上時,∵MN∥PQ,
∴△AMN∽△ABC,
∴

=

,
即

=

,
解得x=7.5,
∴①PQ在△ABC內部時,0<x≤7.5,重疊部分的面積為矩形MNPQ的面積,
y=x•2x=2x
2,
②PQ在△ABC外部時,7.5<x<30,設矩形MNPQ在△ABC內部的長為b,
∵△AMN∽△ABC,
∴

=
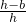
,
即

=

,
解得b=20-

x,
∴y=x(20-

x)=-

x
2+20x,
綜上所述,y與x的關系式為y=

.
分析:(1)設正方形的邊長為a,根據根據相似三角形對應高的比等于相似比列出比例式求解得到a,再根據正方形的面積公式計算即可得解;
(2)先根據相似三角形對應高的比等于相似比列式求出QP在BC上時的x的值,然后分①PQ在△ABC內部時,重疊部分的面積為矩形MNPQ的面積;②PQ在△ABC外部時,設矩形MNPQ在△ABC內部的長為b,根據相似三角形對應高的比等于相似比列出比例式求解得到b,再根據矩形的面積列式整理得到y與x的關系式.
點評:本題考查了相似三角形的判定與性質,矩形的對邊平行且相等,正方形的對邊平行且相等的性質,根據相似三角形的對應高的比等于對應邊的比列出比例式是解題的關鍵.


 =
= ,
, =
= ,
,
 =
= ,
, =
= ,
, =
=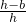 ,
, =
= ,
, x,
x, x)=-
x)=- x2+20x,
x2+20x, .
.

 閱讀材料,解答問題:
閱讀材料,解答問題: