【題目】在一個不透明的盒子中裝有3個形狀大小完全一樣的小球，上面分別有標號1，2，-1，用樹狀圖或列表的方法解決下列問題：
（1）將球攪勻，從盒中一次取出兩個球，求其兩標號互為相反數的概率。
（2）將球攪勻，摸出一個球將其標號記為k，放回后攪勻后再摸出一個球，將其標號記為b.求直線y=kx+b不經過第三象限的概率。
【答案】P（互為相反數）=
；
（2）列表見解析，P（不經過第三象限）=
【解析】分析：(1)列表得到所有可能的結果即可求出兩標號互為相反數的概率;
(2)列表得到所有可能的結果,要注意是不放回事件,即可求出一次函數y=kx+b的圖象不經過第三象限的概率.
本題解析：(1)列表得:
解:(1)列表得:
（2,1） | (-1,1) | |
(1,2) | (-1,2) | |
(1,-1) | (2,-1) |
一共有6種情況,兩次取出小球上的數字兩標號互為相反數的情況有2種,
所以兩標號互為相反數的概率=
;
2)列表得:
b k 結果 | 1 | -1 | 2 |
1 | y=x+1 | y=x-1 | y=x+2 |
-1 | y=-x+1 | y=-x-1 | y=-x+2 |
2 | y=2x+1 | y=2x-1 | y=2x+2 |
一共有9種情況,其中一次函數y=kx+b的圖象不經過第三象限的情況2種,所以其概率=
,
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，將△ABO繞點A順時針旋轉到△AB1C1的位置，點B、O分別落在點B1、C1處，點B1在x軸上，再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置，點C2在x軸上，將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置，點A2在x軸上，依次進行下去…．若點A（ 
，0），B（0，2），則點B2016的坐標為 ． 
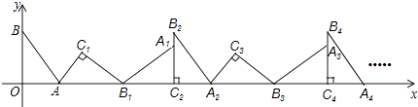
查看答案和解析>>
科目：初中數學 來源： 題型：
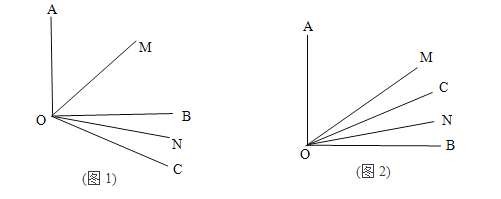
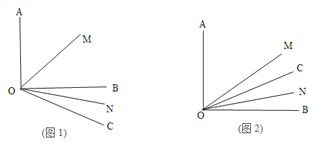
【題目】已知∠AOB=90°，
是銳角，ON平分
，OM平分∠AOB．
（1）如圖1若
=30°，求
的度數？
（2）若射線OC繞著點O運動到∠AOB的內部（如圖2），在（1）的條件下求
的度數；
（3）若∠AOB=
（90°≤
＜180°），
= 
（0°＜
＜90°），請用含有
的式子直接表示上述兩種情況
的度數．
【答案】（1）60°；（2）30°；（3）①∠MON＝
（
＋
），；②∠MON＝
（
－
）．
【解析】試題分析：（1）由于∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，所以可以求得∠MOB和∠NOB的度數，進而求得∠MON的度數；（2）類比（1）的方法求解即可；（3）結合（1）（2）題的計算方法求解即可.
試題解析：
（1）∵OM平分∠AOB，ON平分∠BOC，
∴∠BOM＝
∠AOB，∠BON＝
∠BOC．
∵∠AOB＝90°，∠BOC＝30°，
∴∠BOM＝
×90°＝45°，∠BON＝
×30°＝15°，
∴∠MON＝∠BOM＋∠BON＝45°＋15°＝60°．
（2）由（1）可知：∠BOM＝45°，∠BON＝15°，
∴∠MON＝∠BOM－∠BON＝45°－15°＝30°．
（3）①∠MON＝
（
＋
），②∠MON＝
（
－
）．
點睛：本題主要考查學生角平分線的定義及角的計算的理解和掌握，在解決角與角之間的關系時，要充分利用已知條件和圖中的隱含條件.
【題型】解答題
【結束】
27
【題目】（1）已知線段AB=8cm，在線段AB上有一點C，且BC=4cm，M為線段AC的中點．
①求線段AM的長？
②若點C在線段AB的延長線上，AM的長度又是多少呢？
（2）如圖，AD=
DB，E是BC的中點，BE=
AC=2cm，求DE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等腰Rt△OAA1中，∠OAA1=90°，OA=1，以OA1為直角邊作等腰Rt△OA1A2 ， 以OA2為直角邊作等腰Rt△OA2A3 ， …則OA5的長度為 ．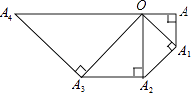 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）閱讀理解：實數
， 
，∵
，∴
，即
。若
（
為定值），則
，當且僅當
時等式成立，即
時， 
，∴當
時， 
取得 值（填“最大”或“最小”）。
（2）理解應用：函數
，當x= 時， 
。
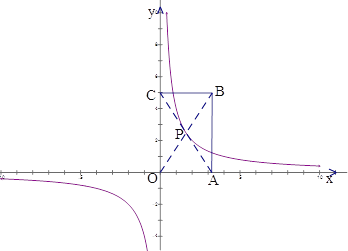
（3）拓展應用：如圖，雙曲線
經過矩形OABC的對角線交點P，求矩形OABC的最小周長。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，點O是邊AC上一個動點，過O作直線MN∥BC．設MN交∠ACB的平分線于點E，交∠ACB的外角平分線于點F． 
（1）求證：OE=OF；
（2）若CE=8，CF=6，求OC的長；
（3）當點O在邊AC上運動到什么位置時，四邊形AECF是矩形？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，點O是邊AC上一個動點，過O作直線MN∥BC．設MN交∠ACB的平分線于點E，交∠ACB的外角平分線于點F．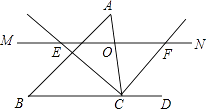 
（1）求證：OE=OF；
（2）若CE=8，CF=6，求OC的長；
（3）當點O在邊AC上運動到什么位置時，四邊形AECF是矩形？并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com