
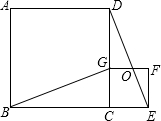
 如圖,四邊形ABCD、CEFG都是正方形,點G在線段CD上,連接BG,DE和FG相交于點O.設AB=a,CG=b(a>b).下列結論:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中結論正確的個數是( )
如圖,四邊形ABCD、CEFG都是正方形,點G在線段CD上,連接BG,DE和FG相交于點O.設AB=a,CG=b(a>b).下列結論:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中結論正確的個數是( )| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
分析 由四邊形ABCD和四邊形CEFG是正方形,根據正方形的性質,即可得BC=DC,CG=CE,∠BCD=∠ECG=90°,則可根據SAS證得①△BCG≌△DCE;然后延長BG交DE于點H,根據全等三角形的對應角相等,求得∠CDE+∠DGH=90°,則可得②BH⊥DE;由△DGO與△DCE相似即可判定③錯誤,證明△EFO∽△DGO,即可求得④正確;即可得出結論.
解答 解:①∵四邊形ABCD和四邊形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,CD∥EF,
∴∠BCG=∠DCE.
在△BCG和△DCE中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCG=∠DCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
故①正確;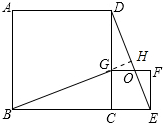
②延長BG交DE于點H,如圖所示:
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正確;
③∵四邊形GCEF是正方形,
∴GF∥CE,
∴$\frac{DG}{DC}=\frac{GO}{CE}$,
$\frac{DG}{GC}=\frac{GO}{CE}$是錯誤的.
故③錯誤;
④∵DC∥EF,
∴△EFO∽△DGO,
∴$\frac{{S}_{△EFO}}{{S}_{△DGO}}$=($\frac{EF}{DG}$)2=($\frac{b}{a-b}$)2=$\frac{{b}^{2}}{(a-b)^{2}}$,
∴(a-b)2•S△EFO=b2•S△DGO.
故④正確;
正確的有3個,故選:B.
點評 本題主要考查正方形的性質、全等三角形的判定和性質及相似三角形的判定和性質,綜合性較強,掌握三角形全等、相似的判定和性質是解題的關鍵.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數學 來源: 題型:選擇題
| A. | 9.8 | B. | 9.6 | C. | 9.5 | D. | 9.4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
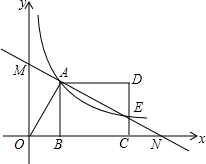 如圖,反比例函數y=$\frac{k}{x}$(x>0)的圖象經過線段OA的端點A,O為原點,作AB⊥x軸于點B,點B的坐標為(2,0),tan∠AOB=$\frac{3}{2}$.
如圖,反比例函數y=$\frac{k}{x}$(x>0)的圖象經過線段OA的端點A,O為原點,作AB⊥x軸于點B,點B的坐標為(2,0),tan∠AOB=$\frac{3}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
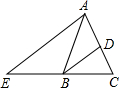 如圖,在△ABC中,AB=AC,BD平分∠ABC交AC于點D,AE∥BD交CB的延長線于點E.若∠BAC=40°,請你選擇圖中現有的一個角并求出它的度數(要求:不添加新的線段,所有給出的條件至少使用一次).
如圖,在△ABC中,AB=AC,BD平分∠ABC交AC于點D,AE∥BD交CB的延長線于點E.若∠BAC=40°,請你選擇圖中現有的一個角并求出它的度數(要求:不添加新的線段,所有給出的條件至少使用一次).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| A型汽車 | B型汽車 | |
| 滿載量(噸) | 5 | 4 |
| 費用(元)/次 | 800 | 600 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
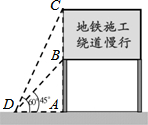 2014年1月3日,長沙軌道交通3號線一期工程正式開工建設,交警隊計劃在一些主要路口設立了交通路況顯示牌(如圖).已知立桿AB高度是3m,從側面D點測得顯示牌頂端C點和底端B點的仰角分別是60°和45°.求路況顯示牌BC的高度.
2014年1月3日,長沙軌道交通3號線一期工程正式開工建設,交警隊計劃在一些主要路口設立了交通路況顯示牌(如圖).已知立桿AB高度是3m,從側面D點測得顯示牌頂端C點和底端B點的仰角分別是60°和45°.求路況顯示牌BC的高度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com