
【題目】一個滑道由滑坡(AB段)和緩沖帶(BC段)組成,如圖所示,滑雪者在滑坡上滑行的距離y(單位:m)和滑行時間t1(單位:s)滿足二次函數關系,并測得相關數據:
滑行時間t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距離y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在緩沖帶上滑行的距離y2(單位:m)和在緩沖帶上滑行時間t2(單位:s)滿足:y2=52t2﹣2t22,滑雪者從A出發在緩沖帶BC上停止,一共用了23s,則滑坡AB的長度( )米
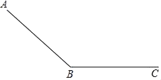
A.270B.280C.375D.450
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() 和一次函數
和一次函數![]() ,其中一次
,其中一次
函數圖象經過(a,b)與(a+1,b+k)兩點.
(1) 求反比例函數的解析式.
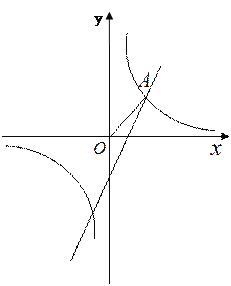
(2) 如圖,已知點A是第一象限內上述兩個函數圖象的交點,求A點坐標.
(3) 利用(2)的結果,請問:在X軸上是否存在點P,使△AOP為等腰三角形?若存在,把符合條件的P點坐標都求出來;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于某一函數給出如下定義:對于任意實數![]() ,當自變量
,當自變量![]() 時,函數
時,函數![]() 關于
關于![]() 的函數圖象為
的函數圖象為![]() ,將
,將![]() 沿直線
沿直線![]() 翻折后得到的函數圖象為
翻折后得到的函數圖象為![]() ,函數
,函數![]() 的圖象由
的圖象由![]() 和
和![]() 兩部分共同組成,則函數
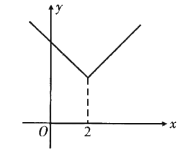
兩部分共同組成,則函數![]() 為原函數的“對折函數”,如函數
為原函數的“對折函數”,如函數![]() (
(![]() )的對折函數為
)的對折函數為![]() .
.
(1)求函數![]() (
(![]() )的對折函數;
)的對折函數;
(2)若點![]() 在函數
在函數![]() (
(![]() )的對折函數的圖象上,求
)的對折函數的圖象上,求![]() 的值;
的值;
(3)當函數![]() (
(![]() )的對折函數與
)的對折函數與![]() 軸有不同的交點個數時,直接寫出
軸有不同的交點個數時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,![]() ,∠DAB=60°,點E是AD邊的中點
,∠DAB=60°,點E是AD邊的中點![]() 點M是AB邊上一動點
點M是AB邊上一動點![]() 不與點A重合
不與點A重合![]() ,延長ME交射線CD于點N,連接MD、AN.
,延長ME交射線CD于點N,連接MD、AN.
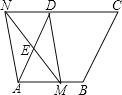
![]() 求證:四邊形AMDN是平行四邊形;
求證:四邊形AMDN是平行四邊形;
![]() 當AM的值為______時,四邊形AMDN是菱形
當AM的值為______時,四邊形AMDN是菱形![]() 并說明理由.
并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
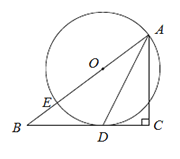
【題目】已知:如圖,在Rt△ABC中,∠C=90°,點E在斜邊AB上,以AE為直徑的⊙O與BC邊相切于點D,連結AD.
(1)求證:AD是∠BAC的平分線;
(2)若AC=3,BC=4,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
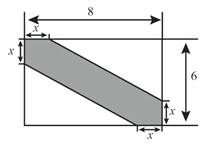
【題目】某景區內有一塊矩形油菜花田地(數據如圖示,單位:m.)現在其中修建一條觀花道(圖中陰影部分)供游人賞花.設改造后剩余油菜花地所占面積為ym2.
(1)求y與x的函數表達式;
(2)若改造后觀花道的面積為13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
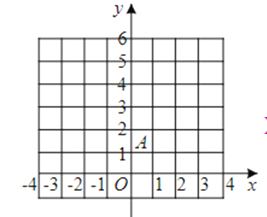
【題目】如圖,在平面直角坐標系xoy中,點A的坐標為(0,1),取一點B(b,0),連接AB,作線段AB的垂直平分線![]() ,過點B作X軸的垂線
,過點B作X軸的垂線![]() ,記
,記![]() ,
,![]() 的交點為P。
的交點為P。
(1)當b=3時,在圖1中補全圖形(尺規作圖,不寫作法,保留作圖痕跡)。
(2)小慧多次取不同數值b,得出相應的點P,并把這些點用平滑的曲線連接起來,發現:這些點P竟然在一條曲線L上。
①設點P的坐標為(x,y),試求y與x之間的關系式,并指出曲線L是哪種曲線。
②設點P到x軸,y軸的距離分別為![]() ,
,![]() ,求
,求![]() +
+![]() 的范圍。當
的范圍。當![]() +
+![]() =8時,求點P的坐標。
=8時,求點P的坐標。
③將曲線在直線y=2下方的部分沿直線y=2向上翻折,得到一條“W”形狀的新曲線,若直線y=kx+3與這條“W”形狀的新曲線有4個交點,直接寫出k的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
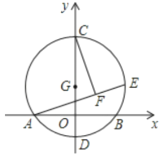
【題目】如圖,以![]() 為圓心,半徑為2的圓與
為圓心,半徑為2的圓與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,
,![]() 兩點,點
兩點,點![]() 為圓
為圓![]() 上一動點,
上一動點,![]() 于
于![]() ,當點
,當點![]() 在圓
在圓![]() 的運動過程中,線段
的運動過程中,線段![]() 的長度的最小值為__________.
的長度的最小值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com