
如圖,一次函數y=kx+b與反比例函數y=
 的圖象相交于A(2,3),B(﹣3,n)兩點.
的圖象相交于A(2,3),B(﹣3,n)兩點.
(1)求一次函數與反比例函數的解析式;
(2)根據所給條件,請直接寫出不等式kx+b>
 的解集;
的解集;
(3)過點B作BC⊥x軸,垂足為C,求S△ABC.
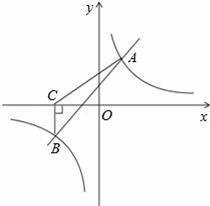

【考點】反比例函數與一次函數的交點問題.
【分析】(1)由一次函數y=kx+b與反比例函數y=
 的圖象相交于A(2,3),B(﹣3,n)兩點,首先求得反比例函數的解析式,則可求得B點的坐標,然后利用待定系數法即可求得一次函數的解析式;
的圖象相交于A(2,3),B(﹣3,n)兩點,首先求得反比例函數的解析式,則可求得B點的坐標,然后利用待定系數法即可求得一次函數的解析式;
(2)根據圖象,觀察即可求得答案;
(3)因為以BC為底,則BC邊上的高為3+2=5,所以利用三角形面積的求解方法即可求得答案.
【解答】解:(1)∵點A(2,3)在y=
 的圖象上,
的圖象上,
∴m=6,
∴反比例函數的解析式為:y=
 ,
,
∵B(﹣3,n)在反比例函數圖象上,
∴n=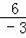
 =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)兩點在y=kx+b上,
∴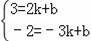
 ,
,
解得: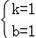
 ,
,
∴一次函數的解析式為:y=x+1;
(2)﹣3<x<0或x>2;
(3)以BC為底,則BC邊上的高AE為3+2=5,
∴S△ABC=
 ×2×5=5.
×2×5=5.
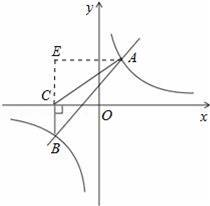

【點評】此題考查了反比例函數與一次函數的交點問題.注意待定系數法的應用是解題的關鍵.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
今年3月21日到武漢大學賞櫻花的人數約為213000人,數213000用科學記數法表示為( )
A.21.3×104 B.213×103 C.2.13×105 D.2.13×104
查看答案和解析>>
科目:初中數學 來源: 題型:
某車的剎車距離y(m)與開始剎車時的速度x(m/s)之間滿足二次函數y=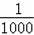
 x2+
x2+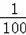
 x(x>0),若該車某次的剎車距離為9m,則開始剎車時的速度為 m/s.
x(x>0),若該車某次的剎車距離為9m,則開始剎車時的速度為 m/s.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com