
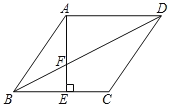
【題目】菱形ABCD中,AE⊥BC于E,交BD于F點,下列結論:
①BF為∠ABE的角平分線;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正確的為( )
.其中正確的為( )
A.①③B.①②④C.①④D.①③④
【答案】D
【解析】
由四邊形ABCD是菱形,即可得BF為∠ABE的角平分線;可得①正確;由當∠ABC=60°時,DF=2BF,可得②錯誤;連接AC,易證得△AOD∽△FAD,由相似三角形的對應邊成比例,可證得AD:DF=OD:AD,繼而可得2AB2=DFDB,即④正確;連接FC,易證得△ABF≌△CBF(SAS),可得∠BCF=∠BAE,AF=CF,然后由正弦函數的定義,可求得④正確.
解:①∵四邊形ABCD是菱形,∴BF為∠ABE的角平分線,
故①正確;
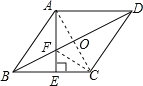
②連接AC交BD于點O.
∵四邊形ABCD是菱形,∴AB=BC=AD,∴當∠ABC=60°時,△ABC是等邊三角形,
即AB=AC,
則DF=2BF.
∵∠ABC的度數不定,∴DF不一定等于2BF;
故②錯誤;
③∵AE⊥BC,AD∥BC,∴AE⊥AD,∴∠FAD=90°.
∵四邊形ABCD是菱形,∴AC⊥BD,OB=OD=![]() DB,AD=AB,∴∠AOD=∠FAD=90°.
DB,AD=AB,∴∠AOD=∠FAD=90°.
∵∠ADO=∠FDO,∴△AOD∽△FAD,∴AD:DF=OD:AD,∴AD2=DFOD,∴AB2=DF![]() DB,
DB,
即2AB2=DFDB;
故③正確;
④連接CF,
在△ABF和△CBF中, ∴△ABF≌△CBF(SAS),∴∠BCF=∠BAE,AF=CF,
∴△ABF≌△CBF(SAS),∴∠BCF=∠BAE,AF=CF,
在Rt△EFC中,sin∠ECF=![]() =
=![]() ,∴sin∠BAE=
,∴sin∠BAE=![]() .
.
故④正確.
故選:D.


科目:初中數學 來源: 題型:
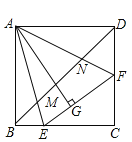
【題目】如圖,在正方形![]() 中,
中,![]() 的頂點
的頂點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 邊上,高
邊上,高![]() 與正方形的邊長相等,連接
與正方形的邊長相等,連接![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,下列說法:①
,下列說法:①![]() ;②連接
;②連接![]() ,
,![]() ,則
,則![]() 為直角三角形;③
為直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,則
,則![]() 的長為
的長為![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
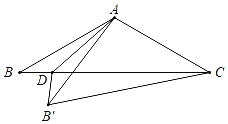
【題目】如圖,在△ABC中,AB=AC=![]() ,∠B=30°,D是BC上一點,連接AD,把△ABD沿直線AD折疊,點B落在B′處,連接B'C,若△AB'C是直角三角形,則BD的長為_____.
,∠B=30°,D是BC上一點,連接AD,把△ABD沿直線AD折疊,點B落在B′處,連接B'C,若△AB'C是直角三角形,則BD的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】家住重慶兩相鄰小區的小明和小華在一次數學課后,進行了一次數學實踐活動.如圖,在同一水平面從左往右依次是小明家所在的居民樓、小華家所在的小洋房、背靠小華家的一座小山,實踐內容為測量小山的高度,家住頂樓的小明在窗戶A處測得小山山頂的一棵大樹頂端E的俯角為10°,小華在自家樓下C處測得小明家窗戶A處的仰角為37°,且測得坡面CD的坡度i=1:2,已知兩家水平距離BC=120米,大樹高度DE=3米,則小山山頂D到水平面BF的垂直高度約為( )(精確到0.1米,參考數據sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)

A.55.0米B.50.3米C.48.1 米D.57.3米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在函數的學習中,我們經歷了“確定函數表法式﹣畫函數圖象﹣利用函數圖象研究函數性質﹣利用圖象解決問題”的學習過程.在畫函數圖象時,我們常常通過描點或平移或翻折的方法畫函數圖象.小明根據學到的函數知識探究函數y1=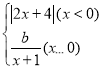 的圖象與性質并利用圖象解決問題.小明列出了如表y1與x的幾組對應的值:
的圖象與性質并利用圖象解決問題.小明列出了如表y1與x的幾組對應的值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
(1)根據表格中x、y1的對應關系可得m=______,n=______;
(2)在平面直角坐標系中,描出表格中各點,兩出該函數圖象;根據函數圖象,寫出該函數的一條性質______.
(3)當函數y1的圖象與直線y2=mx+1有三個交點時,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
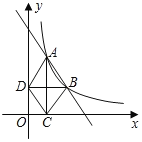
【題目】如圖,在直角坐標平面內,函數y=![]() (x>0,m是常數)的圖象經過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD,DC,CB.
(x>0,m是常數)的圖象經過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD,DC,CB.
(1)求反比例函數的解析式;
(2)若△ABD的面積為4,求點B的坐標;
(3)求證:DC![]() AB.
AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加快城鄉對接,建設全域美麗鄉村,某地區對A、B兩地間的公路進行改建.如圖,A、B兩地之間有一座山,汽車原來從A地到B地需途徑C地沿折線ACB行駛,現開通隧道后,汽車可直接沿直線AB行駛.已知BC=80千米,∠A=45°,∠B=30°.
(1)開通隧道前,汽車從A地到B地大約要走多少千米?
(2)開通隧道后,汽車從A地到B地大約可以少走多少千米?(結果精確到0.1千米)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
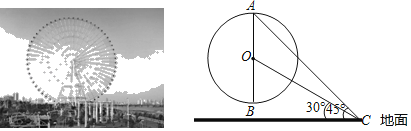
【題目】“天空之城”摩天輪,位于寧波市杭州灣新區歡樂世界.摩天輪高約126米(最高點到地面的距離).如圖,點O是摩天輪的圓心,AB是其垂直于地面的直徑,小明在地面C處用測角儀測得摩天輪最高點A的仰角為45°,測得圓心O的仰角為30°,求摩天輪的半徑.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是![]() 的直徑,點P在BA的延長線上,PD切
的直徑,點P在BA的延長線上,PD切![]() 于點D,過點B作
于點D,過點B作![]() ,交PD的延長線于點C,連接AD并延長,交BE于點E.
,交PD的延長線于點C,連接AD并延長,交BE于點E.
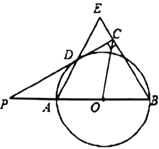
(Ⅰ)求證:AB=BE;
(Ⅱ)連結OC,如果PD=2![]() ,∠ABC=60°,求OC的長.
,∠ABC=60°,求OC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com