【題目】如圖，直線y=2x+6與反比例函數y=
（k＞0）的圖象交于點A（1，m），與x軸交于點B，平行于x軸的直線y=n（0＜n＜6）交反比例函數的圖象于點M，交AB于點N，連接BM．
（1）求m的值和反比例函數的表達式；
（2）直線y=n沿y軸方向平移，當n為何值時，△BMN的面積最大？
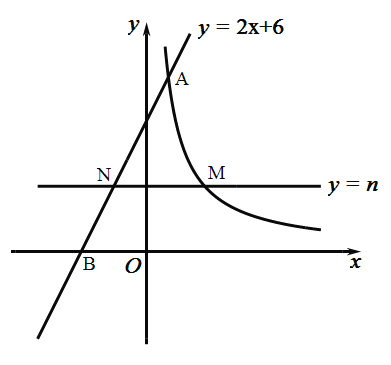
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】現代互聯網技術的廣泛應用，催生了快遞行業的高度發展．據調查，太原市某家小型“大學生自主創業”的快遞公司，今年九月份與十一月份完成投遞的快遞總件數分別為10萬件和12．1萬件．現假定該公司每月投遞的快遞總件數的增長率相同．
（1）求該快遞公司投遞總件數的月平均增長率；
（2）如果平均每人每月最多可投遞0．6萬件，那么該公司現有的21名快遞業務員能否完成今年十二月份的快遞投遞任務?如果不能，請問至少需要增加幾名業務員?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】近代統計學的發展起源于二十世紀初，它是在概率論的基礎上發展起來的，但統計性質的工作可以追溯到遠古的“結繩記事”和《二十四史》中大量的關于我國人口、錢糧、水文、天文、地震等資料的記錄．現代數理統計的奠基人是英國數學家和生物學家費希爾，畢業于劍橋大學，長期在農業試驗站做生物實驗．費爾希在高等植物基因性狀研究實驗中，從若干紫花與白花中各隨機抽取20株測量高度（植株正常高度
的取值范圍為
），過程如下：
收集數據（單位：
）：
紫花：42，42，28，54，29，52，44，36，39，49，33，40，35，52，29，32，51，55，42，38
白花植株高度為的數據有：35，37，37，38，39，40，42，42
整理數據：
數據分為六組：
，
，
，
，
，
組別 |
|
|
|
|
|
|
紫花數量 | 3 | 2 |
| 5 | 1 | 5 |
分析數據：
植株 | 平均數 | 眾數 | 中位數 | 方差 |
紫花 | 41．1 | 42 | 41 | 8．8 |
白花 | 40．25 | 43 |
| 7．2 |
應用數據：
（1）請寫出表中
，
；
（2）估計500株紫花中高度正常的有多少株？
（3）結合上述數據信息，請判斷哪種花長勢更均勻，并說明理由（一條理由即可）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于平面直角坐標系xOy中的點P和⊙C，給出如下定義：若⊙C上存在一個點M，使得PM = MC，則稱點P為⊙C的“等徑點”．已知點D
，E
，F
．
（1）當⊙O的半徑為1時，
①在點D，E，F中，⊙O的“等徑點”是 ；
②作直線EF，若直線EF上的點T（m，n）是⊙O的“等徑點”，求m的取值范圍．
（2）過點E作EG⊥EF交x軸于點G，若△EFG上的所有點都是某個圓的“等徑點”，求這個圓的半徑r的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】袋中裝有除數字不同其它都相同的六個小球，球上分別標有數字1，2，3，4，5，6．
（1）從袋中摸出一個小球，求小球上數字小于3的概率；
（2）將標有1，2，3數字的小球取出放入另外一個袋中，分別從兩袋中各摸出一個小球，
求數字之和為偶數的概率．（要求用列表法或畫樹狀圖求解）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了慶祝中華人民共和國成立70周年，某市決定開展“我和祖國共成長”主題演講比賽，某中學將參加本校選拔賽的40名選手的成績（滿分為100分，得分為正整數且無滿分，最低為75分）分成五組，并繪制了下列不完整的統計圖表．
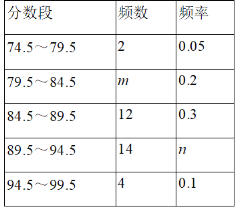
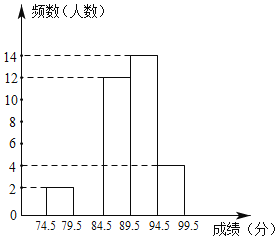
（1）表中m＝ ，n＝ ；
（2）請在圖中補全頻數直方圖；
（3）甲同學的比賽成績是40位參賽選手成績的中位數，據此推測他的成績落在 分數段內；
（4）選拔賽中，成績在94.5分以上的選手，男生和女生各占一半，學校從中隨機確定2名選手參加全市決賽，請用列舉法或樹狀圖法求恰好是一名男生和一名女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某養殖戶長期承包一口魚糖養魚，每年養殖一批，從魚苗放入養到成品需要300天，魚糖承包費用每年5000元，他記錄了前幾年平均每天投入飼料量（單位：kg）與年底成品魚（達到一定規格可以銷售）產量之間的關系如下表：
平均每天投入飼料（kg） | 20 | 25 | 30 | 40 | 50 | 60 | 70 | 80 |
成品魚產量（kg） | 2800 | 3000 | 3200 | 3600 | 3900 | 4000 | 3900 | 3600 |
（1）請用適當的函數模型描述平均每天投入飼料數量與成品魚產量之間的關系；
（2）如果今年的飼料價格為1．6元/kg，成品魚銷售價為20元/kg，魚苗費用4000元，假設養成的成品魚全部都能按此價格賣出．請建立適當的函數模型平均每天投入飼料多少千克時，該養殖戶當年在該魚糖養殖這種魚獲得的利潤最多，最多利潤是多少元？（利潤＝銷售收入﹣飼料成本﹣魚糖承包費﹣魚苗成本）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸，
軸分別交于點
，經過點的拋物線
與軸的另一個交點為點
，點
是拋物線上一點，過點作
軸于點
，連接
，設點的橫坐標為
.
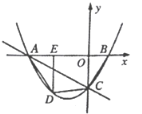
求拋物線的解析式；
當點在第三象限，設
的面積為
，求與的函數關系式，并求出的最大值及此時點的坐標；
連接
，若
,請直接寫出此時點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，BC＝9，∠ABC的平分線BF交AC于點F，點D、點E分別是邊AB、AC上的點，若
，則BD﹣DE的值為（ ）
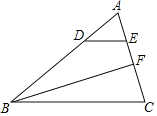
A.3B.3．5C.4D.4．5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
