
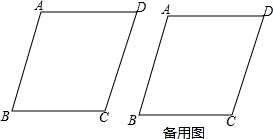
分析 (1)連接BD、AC交于點O,作AH⊥BC于H,由菱形的性質得出AO=OC=3,BO=4,由△ABC的面積求出AH=$\frac{24}{5}$,由勾股定理得出BH,即可得出結果;
(2)由菱形的性質得出∠FAC=∠ACB,證出△ABC∽△ECF,得出對應邊成比例$\frac{AB}{CE}$=$\frac{AC}{EF}$,求出EF,由平行線得出△MBC∽△MAF,得出$\frac{BM}{AM}$=$\frac{BC}{AF}$=$\frac{25}{36}$,即可得出結果;
(3)作EM⊥BC于M,作EG∥BC交CF于G,由(1)知cos∠B=$\frac{7}{25}$,BE=x,得出BM=$\frac{7}{25}$x,由勾股定理得出EM=$\frac{24}{25}$x,CE=$\sqrt{E{M}^{2}+M{C}^{2}}$=$\sqrt{{x}^{2}-\frac{14}{5}x+25}$,由平行線得出∠GEC=∠ECB,$\frac{BC}{EG}=\frac{BM}{ME}$,證出△BCE∽△CEG,得出對應邊成比例$\frac{BC}{CE}=\frac{CE}{EG}$,得出EG=$\frac{C{E}^{2}}{BC}$=$\frac{5{x}^{2}-14x+125}{25}$,代入比例式即可得出y關于x的函數解析式為y=$\frac{125}{5x-14}$($\frac{14}{5}$<x≤5).
解答 解:(1)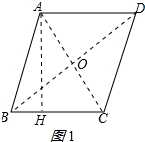 連接BD、AC交于點O,作AH⊥BC于H,如圖1所示:
連接BD、AC交于點O,作AH⊥BC于H,如圖1所示:
則AO=OC=3,BO=4,
∵S△ABC=$\frac{1}{2}$BC×AH=$\frac{1}{2}$AC×BO=$\frac{1}{2}$×6×4=12,
∴$\frac{1}{2}$×5×AH=12,
解得:AH=$\frac{24}{5}$,
由勾股定理得:BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-(\frac{24}{5})^{2}}$=$\frac{7}{5}$,
∴cos∠B=$\frac{BH}{AB}$=$\frac{\frac{7}{5}}{5}$=$\frac{7}{25}$;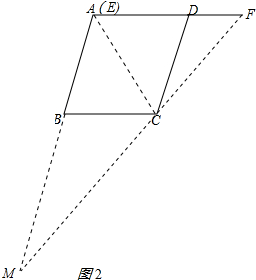
(2)當點E與點A重合時,符合題意的圖形,如圖2所示:
∵四邊形ABCD為菱形,
∴∠FAC=∠ACB,
∵∠ECF=∠B,
∴△ABC∽△ECF,
∴$\frac{AB}{CE}$=$\frac{AC}{EF}$,即$\frac{5}{6}$=$\frac{6}{EF}$,
解得:EF=$\frac{36}{5}$,
∵BC∥AF,
∴△MBC∽△MAF,
∴$\frac{BM}{AM}$=$\frac{BC}{AF}$=$\frac{5}{\frac{36}{5}}$=$\frac{25}{36}$,
∴$\frac{BM}{BM+5}$=$\frac{25}{36}$,
解得:BM=$\frac{125}{11}$;
(3)作EH⊥BC于H,作EG∥BC交CF于G,如圖3所示: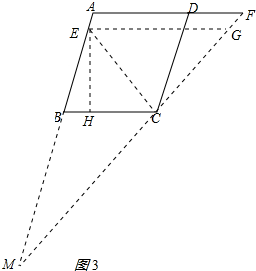
由(1)知cos∠B=$\frac{7}{25}$,BE=x,
∴BH=$\frac{7}{25}$x,EH=$\sqrt{B{E}^{2}-B{H}^{2}}$=$\sqrt{{x}^{2}-(\frac{7}{25}x)^{2}}$=$\frac{24}{25}$x,
∴CE=$\sqrt{E{H}^{2}+C{H}^{2}}$=$\sqrt{(5-\frac{7}{25}x)^{2}+(\frac{24}{25}x)^{2}}$=$\sqrt{{x}^{2}-\frac{14}{5}x+25}$,
∵EG∥BC,
∴∠GEC=∠ECB,$\frac{BC}{EG}=\frac{BM}{ME}$,
∴△BCE∽△CEG,
∴$\frac{BC}{CE}=\frac{CE}{EG}$,
則EG=$\frac{C{E}^{2}}{BC}$=$\frac{5{x}^{2}-14x+125}{25}$,
∴$\frac{5}{\frac{5{x}^{2}-14x+125}{25}}=\frac{y}{x+y}$,
整理得:y=$\frac{125}{5x-14}$,
即y關于x的函數解析式為y=$\frac{125}{5x-14}$($\frac{14}{5}$<x≤5).
點評 本題是相似形綜合題目,考查了菱形的性質、相似三角形的判定與性質、平行線的性質、勾股定理、三角函數等知識;本題綜合性強,難度較大,特別是(3)中,需要運用勾股定理和證明三角形相似得出比例式才能得出結果.


科目:初中數學 來源: 題型:填空題
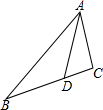 如圖,在△ABC中,點D在邊BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,則S△ACD=$\frac{3}{2}$.
如圖,在△ABC中,點D在邊BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,則S△ACD=$\frac{3}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 任意打開一本200頁的數學書,恰好是第50頁 | |
| B. | 打開電視機,任選一個頻道,正在播放足球賽 | |
| C. | 在空曠的操場上向上拋出的籃球一定會下落 | |
| D. | 陰天一定會下雨 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 13道 | B. | 14道 | C. | 15道 | D. | 16道 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com