
【題目】已知四邊形ABCD中,EF分別是AB、AD邊上的點,DE與CF交于點G.
(1)如圖1,若四邊形ABCD是正方形,且DE⊥CF,求證:DE=CF;

(2)如圖2,若四邊形ABCD是矩形,且DE⊥CF,求證:![]() ;
;

(3)如圖3,若四邊形ABCD是平行四邊形,當∠B=∠EGF時,第(2)問的結論是否成立?若成立給予證明;若不成立,請說明理由.

【答案】(1)證明見解析;(2)證明見解析;(3)當∠B=∠EGF時,![]() 成立,證明見解析.
成立,證明見解析.
【解析】
(1)由四邊形ABCD為正方形,利用正方形的性質得到一對角為直角,相等,且AD=DC,利用同角的余角相等得到一對角相等,利用AAS得到三角形ADE與三角形DCF全等,利用全等三角形對應邊相等即可得證;
(2)由四邊形ABCD為矩形,得到一對直角相等,利用同角的余角相等得到一對角相等,利用兩對角相等的三角形相似得到三角形ADE與三角形DCF相似,利用相似三角形對應邊成比例即可得證;
(3)當∠B=∠EGF時,![]() 成立,理由為:如圖3,在AD的延長線上取點M,使CM=CF,利用平行線的性質,以及同角的補角相等得到三角形ADE與三角形DCM相似,利用相似三角形對應邊成比例即可得證.
成立,理由為:如圖3,在AD的延長線上取點M,使CM=CF,利用平行線的性質,以及同角的補角相等得到三角形ADE與三角形DCM相似,利用相似三角形對應邊成比例即可得證.
(1)∵四邊形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,
∴∠AED=∠CFD,
∴△ADE≌△DCF,
∴DE=CF
(2)∵四邊形ABCD是矩形,
∴∠A=∠ADC=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,∠DCF+∠CFD=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴![]()
(3)解:當∠B=∠EGF時, ![]() 成立,
成立,
證明:如圖3,在AD的延長線上取點M,使CM=CF,
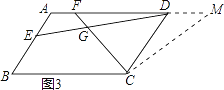
則∠CMF=∠CFM,
∵AB∥CD,
∴∠A=∠CDM,
∵AD∥BC,
∴∠B+∠A=180°,
∵∠B=∠EGF,
∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,
∴ ![]() ,即
,即 ![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,直線l:y=![]() x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=
x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=![]() x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
(1)求n的值和拋物線的解析式;
(2)點D在拋物線上,DE∥y軸交直線l于點E,點F在直線l上,且四邊形DFEG為矩形(如圖2),設點D的橫坐標為t(0<t<4),矩形DFEG的周長為p,求p與t的函數關系式以及p的最大值;
(3)將△AOB繞平面內某點M旋轉90°或180°,得到△A1O1B1,點A、O、B的對應點分別是點A1、O1、B1.若△A1O1B1的兩個頂點恰好落在拋物線上,那么我們就稱這樣的點為“落點”,請直接寫出“落點”的個數和旋轉180°時點A1的橫坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】放假時小華父子倆一同出發去露營,步行途中小華發現睡袋忘拿了跑步回家取,之后立刻返程跑步追趕爸爸,期間爸爸繼續步行去往露營地,會合時爸爸發現還需要探照燈,為節約時間爸爸乘車回家去拿,小華繼續步行至露營地,爸爸拿到探照燈后乘車也到了終點(假定步行、跑步和汽車均為勻速,且二人取物品時間忽略不計),二人之間的距離s(米)與他們出發時間t(分鐘)之間的關系如圖所示,則當爸爸到家時,小華與露營地相距_____米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】市教育局在全市中小學推廣某學校“品格教育”科研成果,其中“敬老孝親”是“品格教育”亮點之一. 重陽節(農歷九月初九)快到了,某校八年級(1)班班委發起為老人們獻上真摯的節日祝福活動,決定全班同學利用課余時間去賣鮮花籌集慰問金.已知同學們從花店按每支1.5元買進鮮花,并按每支4.5元賣出.
(1)求同學們賣出鮮花的銷售額![]() (元)與銷售量
(元)與銷售量![]() (支)之間的函數關系式;
(支)之間的函數關系式;
(2)若從花店購買鮮花的同時,還總共用去40元購買包裝材料,求所籌集的慰問金![]() (元)與銷售量
(元)與銷售量![]() (支)之間的函數關系式;若要籌集不少于500元的慰問金,則至少要賣出鮮花多少支?(慰問金 = 銷售額 - 成本)
(支)之間的函數關系式;若要籌集不少于500元的慰問金,則至少要賣出鮮花多少支?(慰問金 = 銷售額 - 成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索規律:下列圖案是山西晉商大院窗格的一部分,其中“○”代表窗紙上所貼的剪紙,隨著基本圖案的增加所貼剪紙“○”的總個數也在發生變化.

(1)填寫下表:
第 | 1 | 2 | 3 | 4 | …… |
“○”的總個數 | …… |
(2)請你寫出第![]() 個圖案中“○”的總個數
個圖案中“○”的總個數![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,正比例函數
中,正比例函數![]() 與一次函數
與一次函數![]() 的圖象相交于點
的圖象相交于點![]() .過點
.過點![]() 作
作![]() 軸的垂線,分別交正比例函數的圖象于點
軸的垂線,分別交正比例函數的圖象于點![]() ,交一次函數的圖象于點
,交一次函數的圖象于點![]() ,連接
,連接![]() .
.

(1)求這兩個函數的表達式;
(2)求![]() 的面積;
的面積;
(3)在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使
,使![]() 為直角三角形?若存在,請直接寫出滿足條件的所有
為直角三角形?若存在,請直接寫出滿足條件的所有![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是線段
是線段![]() 邊上的任意一點(不含端點
邊上的任意一點(不含端點![]() 、
、![]() ),連接
),連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() .
.

![]() 在線段
在線段![]() 上是否存在不同于
上是否存在不同于![]() 的點
的點![]() ,使得
,使得![]() ?若存在,求線段
?若存在,求線段![]() 與
與![]() 之間的數量關系;若不存在,請說明理由;
之間的數量關系;若不存在,請說明理由;
![]() 當點
當點![]() 在
在![]() 上運動時,對應的點
上運動時,對應的點![]() 也隨之在
也隨之在![]() 上運動,求
上運動,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點.
(1)求證:△ACE≌△BCD;
(2)求證:2CD2=AD2+DB2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形的邊長都是1,每個小格的頂點叫做格點.

(1)在圖1中以格點為頂點畫一個面積為5的正方形;
(2)在圖2中以格點為頂點畫一個三角形,使三角形三邊長分別為2、![]() 、
、![]() ;
;
(3)如圖3,A、B、C是小正方形的頂點,求∠ABC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com