解:(1)
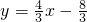
,
當(dāng)y=0時(shí),x=2,
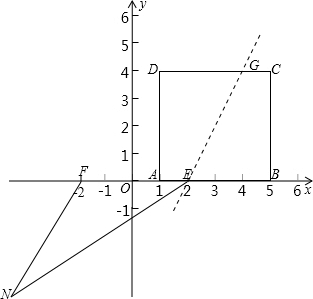
∴E(2,0),
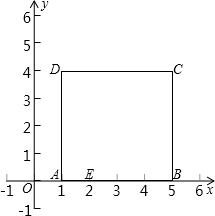
由已知可得:AD=AB=BC=DC=4,AB∥DC,
∴四邊形AECD是梯形,
∴四邊形AECD的面積S=

×(2-1+4)×4=10,
答:四邊形AECD的面積是10.
(2)在DC上取一點(diǎn)G,使CG=AE=1,
則S
t梯形AEGD=S
梯形EBCG,
∴G點(diǎn)的坐標(biāo)為(4,4),
設(shè)直線(xiàn)l的解析式是y=kx+b,代入得:
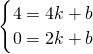
,
解得:
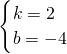
,
即:y=2x-4,
答:直線(xiàn)l的解析式是y=2x-4.
(3)∵直線(xiàn)l
1經(jīng)過(guò)點(diǎn)F(
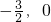
)且與直線(xiàn)y=3x平行,
設(shè)直線(xiàn)1
1的解析式是y
1=kx+b,
則:k=3,
代入得:0=3×(-

)+b,
解得:b=

,
∴y
1=3x+

已知將(2)中直線(xiàn)l沿著y軸向上平移1個(gè)單位,則所得的直線(xiàn)的解析式是y=2x-4+1,
即:y=2x-3,
當(dāng)y=0時(shí),x=

,
∴M(

,0),
解方程組
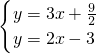
得:
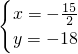
,
即:N(-

,-18),
S
△NMF=

×[

-(-

)]×|-18|=27.
答:△NMF的面積是27.
分析:(1)先求出E點(diǎn)的坐標(biāo),根據(jù)梯形的面積公式即可求出四邊形AECD的面積;
(2)根據(jù)已知求出直線(xiàn)1上點(diǎn)G的坐標(biāo),設(shè)直線(xiàn)l的解析式是y=kx+b,把E、G的坐標(biāo)代入即可求出解析式;
(3)根據(jù)直線(xiàn)l
1經(jīng)過(guò)點(diǎn)F(
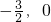
)且與直線(xiàn)y=3x平行,知k=3,把F的坐標(biāo)代入即可求出b的值即可得出直線(xiàn)1
1,同理求出解析式y(tǒng)=2x-3,進(jìn)一步求出M、N的坐標(biāo),利用三角形的面積公式即可求出△MNF的面積.
點(diǎn)評(píng):本題主要考查了一次函數(shù)的特點(diǎn),待定系數(shù)法求一次函數(shù)的解析式,一次函數(shù)圖象上點(diǎn)的特征,平移的性質(zhì)等知識(shí)點(diǎn),解此題的關(guān)鍵是能綜合運(yùn)用上面的知識(shí)求一次函數(shù)的解析式.

 的坐標(biāo)是(1,0).
的坐標(biāo)是(1,0).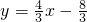 經(jīng)過(guò)點(diǎn)C,且與x軸交于點(diǎn)E,求四邊形AECD的面積;
經(jīng)過(guò)點(diǎn)C,且與x軸交于點(diǎn)E,求四邊形AECD的面積;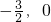 )且與直線(xiàn)y=3x平行.將(2)中直線(xiàn)l沿著y軸向上平移1個(gè)單位,交x軸于點(diǎn)M,交直線(xiàn)l1于點(diǎn)N,求△NMF的面積.
)且與直線(xiàn)y=3x平行.將(2)中直線(xiàn)l沿著y軸向上平移1個(gè)單位,交x軸于點(diǎn)M,交直線(xiàn)l1于點(diǎn)N,求△NMF的面積.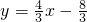 ,
,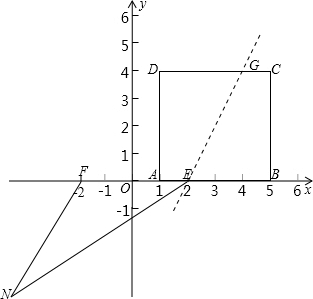
 ×(2-1+4)×4=10,
×(2-1+4)×4=10,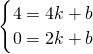 ,
,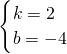 ,
,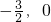 )且與直線(xiàn)y=3x平行,
)且與直線(xiàn)y=3x平行, )+b,
)+b, ,
,
 ,
, ,0),
,0),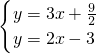 得:
得: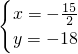 ,
, ,-18),
,-18), ×[
×[ -(-
-(- )]×|-18|=27.
)]×|-18|=27.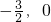 )且與直線(xiàn)y=3x平行,知k=3,把F的坐標(biāo)代入即可求出b的值即可得出直線(xiàn)11,同理求出解析式y(tǒng)=2x-3,進(jìn)一步求出M、N的坐標(biāo),利用三角形的面積公式即可求出△MNF的面積.
)且與直線(xiàn)y=3x平行,知k=3,把F的坐標(biāo)代入即可求出b的值即可得出直線(xiàn)11,同理求出解析式y(tǒng)=2x-3,進(jìn)一步求出M、N的坐標(biāo),利用三角形的面積公式即可求出△MNF的面積.


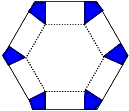 如圖,將邊長(zhǎng)為6cm的正六邊形紙板的六個(gè)角各剪切去一個(gè)全等的四邊形,再沿虛線(xiàn)折起,做成一個(gè)無(wú)蓋直六棱柱紙盒,使側(cè)面積等于底面積,被剪去的六個(gè)四邊形的面積和為
如圖,將邊長(zhǎng)為6cm的正六邊形紙板的六個(gè)角各剪切去一個(gè)全等的四邊形,再沿虛線(xiàn)折起,做成一個(gè)無(wú)蓋直六棱柱紙盒,使側(cè)面積等于底面積,被剪去的六個(gè)四邊形的面積和為
 (2013•豐南區(qū)一模)如圖,將邊長(zhǎng)為a的正六邊形A1A2A3A4A5A6在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng)為
(2013•豐南區(qū)一模)如圖,將邊長(zhǎng)為a的正六邊形A1A2A3A4A5A6在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng)為 (2012•惠城區(qū)模擬)如圖,將邊長(zhǎng)為a的正六邊形A1A2A3A4A5A6在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng)
(2012•惠城區(qū)模擬)如圖,將邊長(zhǎng)為a的正六邊形A1A2A3A4A5A6在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng) 如圖,將邊長(zhǎng)為3的正六邊形A1A2A3A4A5A6,在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng)為( )
如圖,將邊長(zhǎng)為3的正六邊形A1A2A3A4A5A6,在直線(xiàn)l上由圖1的位置按順時(shí)針?lè)较蛳蛴易鳠o(wú)滑動(dòng)滾動(dòng),當(dāng)A1第一次滾動(dòng)到圖2位置時(shí),頂點(diǎn)A1所經(jīng)過(guò)的路徑的長(zhǎng)為( )