
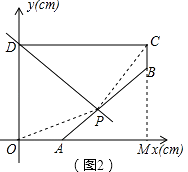
【題目】如圖1,A、D分別在x軸和y軸上,CD∥x軸,BC∥y軸.點P從D點出發,以1cm/s的速度,沿五邊形DOABC的邊勻速運動一周.記順次連接P、O、D三點所圍成圖形的面積為Scm2 , 點P運動的時間為ts.已知S與t之間的函數關系如圖2中折線段OEFGHI所示.
(1)求A、B兩點的坐標;
(2)若直線PD將五邊形OABCD分成面積相等的兩部分,求直線PD的函數關系式.
【答案】
(1)
解:連接AD,設點A的坐標為(a,0),
由圖2知,DO+OA=6cm,則DO=6﹣AO=6﹣a,
由圖2知S△AOD=4,
∴ ![]() DOAO=
DOAO= ![]() a(6﹣a)=4,
a(6﹣a)=4,
整理得:a2﹣6a+8=0,
解得a=2或a=4,
由圖2知,DO>3,
∴AO<3,
∴a=2,
∴A的坐標為(2,0),
D點坐標為(0,4),
在圖1中,延長CB交x軸于M,
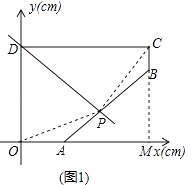
由圖2,知AB=5cm,CB=1cm,
∴MB=3,
∴AM= ![]() =4.
=4.
∴OM=6,
∴B點坐標為(6,3)
(2)
解:因為P在OA、BC、CD上時,直線PD都不能將五邊形OABCD分成面積相等的兩部分,
所以只有點P一定在AB上時,才能將五邊形OABCD分成面積相等的兩部分,
設點P(x,y),連PC、PO,則
S四邊形DPBC=S△DPC+S△PBC= ![]() S五邊形OABCD=
S五邊形OABCD= ![]() (S矩形OMCD﹣S△ABM)=9,
(S矩形OMCD﹣S△ABM)=9,
∴ ![]() ×6×(4﹣y)+
×6×(4﹣y)+ ![]() ×1×(6﹣x)=9,
×1×(6﹣x)=9,
即x+6y=12,
同理,由S四邊形DPAO=9可得2x+y=9,
由 ![]() ,
,
解得x= ![]() ,y=
,y= ![]() .
.
∴P( ![]() ,
, ![]() ),
),
設直線PD的函數關系式為y=kx+4(k≠0),
則 ![]() =
= ![]() k+4,
k+4,
∴k=﹣ ![]() ,
,
∴直線PD的函數關系式為y=﹣ ![]() x+4.
x+4.
【解析】(1)先連接AD,設點A的坐標為(a,0),由圖2得出DO=6﹣AO和S△AOD=4,即可得出 ![]() DOAO=4,從而得出a的值,再根據圖2得出A的坐標,再延長CB交x軸于M,根據D點的坐標得出AB=5cm,CB=1cm,即可求出AM=
DOAO=4,從而得出a的值,再根據圖2得出A的坐標,再延長CB交x軸于M,根據D點的坐標得出AB=5cm,CB=1cm,即可求出AM= ![]() =4,從而得出點B的坐標.(2)先設點P(x,y),連PC、PO,得出S四邊形DPBC的面積,再進行整理,即可得出x與y的關系,再由A,B點的坐標,求出直線AB的函數關系式,從而求出x、y的值,即可得出P點的坐標,再設直線PD的函數關系式為y=kx+4,求出K的值,即可得出直線PD的函數關系式.
=4,從而得出點B的坐標.(2)先設點P(x,y),連PC、PO,得出S四邊形DPBC的面積,再進行整理,即可得出x與y的關系,再由A,B點的坐標,求出直線AB的函數關系式,從而求出x、y的值,即可得出P點的坐標,再設直線PD的函數關系式為y=kx+4,求出K的值,即可得出直線PD的函數關系式.
【考點精析】利用一次函數的性質和一次函數的圖象和性質對題目進行判斷即可得到答案,需要熟知一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠.


 互動英語系列答案
互動英語系列答案 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2cm,∠A=60°. ![]() 是以點A為圓心、AB長為半徑的弧,
是以點A為圓心、AB長為半徑的弧, ![]() 是以點B為圓心、BC長為半徑的弧.則陰影部分的面積為cm2 .
是以點B為圓心、BC長為半徑的弧.則陰影部分的面積為cm2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
(1)如圖1,在△ABC中,BA=BC,D,E是AC邊上的兩點,且滿足∠DBE= ![]() ∠ABC(0°<∠CBE<∠
∠ABC(0°<∠CBE<∠ ![]() ABC).以點B為旋轉中心,將△BEC按逆時針旋轉∠ABC,得到△BE′A(點C與點A重合,點E到點E′處)連接DE′, 求證:DE′=DE.
ABC).以點B為旋轉中心,將△BEC按逆時針旋轉∠ABC,得到△BE′A(點C與點A重合,點E到點E′處)連接DE′, 求證:DE′=DE.
(2)如圖2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC邊上的兩點,且滿足∠DBE= ![]() ∠ABC(0°<∠CBE<45°). 求證:DE2=AD2+EC2 .
∠ABC(0°<∠CBE<45°). 求證:DE2=AD2+EC2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在1,2,3,4,5這五個數中,先任意選出一個數a,然后在余下的數中任意取出一個數b,組成一個點(a,b),求組成的點(a,b)恰好橫坐標為偶數且縱坐標為奇數的概率.(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明有2件上衣,分別為紅色和藍色,有3條褲子,其中2條為藍色、1條為棕色.小明任意拿出1件上衣和1條褲子穿上.請用畫樹狀圖或列表的方法列出所有可能出現的結果,并求小明穿的上衣和褲子恰好都是藍色的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據悉,2013年財政部核定海南省發行的60億地方政府“債券資金”,全部用于交通等重大項目建設.以下是60億“債券資金”分配統計圖: 
(1)請將條形統計圖補充完整;
(2)在扇形統計圖中,a= , b=(都精確到0.1);
(3)在扇形統計圖中,“教育文化”對應的扇形圓心角的度數為°(精確到1°)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3, 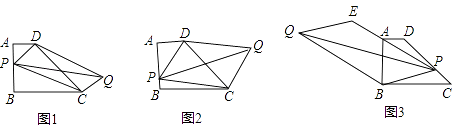
問題1:如圖1,P為AB邊上的一點,以PD,PC為邊作平行四邊形PCQD,請問對角線PQ,DC的長能否相等,為什么?
問題2:如圖2,若P為AB邊上一點,以PD,PC為邊作平行四邊形PCQD,請問對角線PQ的長是否存在最小值?如果存在,請求出最小值,如果不存在,請說明理由.
問題3:若P為AB邊上任意一點,延長PD到E,使DE=PD,再以PE,PC為邊作平行四邊形PCQE,請探究對角線PQ的長是否也存在最小值?如果存在,請求出最小值,如果不存在,請說明理由.
問題4:如圖3,若P為DC邊上任意一點,延長PA到E,使AE=nPA(n為常數),以PE、PB為邊作平行四邊形PBQE,請探究對角線PQ的長是否也存在最小值?如果存在,請求出最小值,如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com