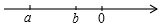Question

9．已知實數a、b在數軸上的對應點如圖所示，化簡$\sqrt{{a}^{2}}$+|a+b|+|$\sqrt{2}$-a|-$\sqrt{（b-\sqrt{2}）^{2}}$．

Answer 1

分析 根據數軸判斷a、a+b、$\sqrt{2}$-a、b-$\sqrt{2}$與0的大小，然后根據絕對值的性質進行化簡即可．

解答 解：由數軸可知：a＜b＜0，
∴a＜0，a+b＜0，
∵$\sqrt{2}$＞0，
∴$\sqrt{2}$-a＞0，b-$\sqrt{2}$＜0，
∴原式=|a|-（a+b）+$\sqrt{2}$-a-|b-$\sqrt{2}$|
=-a-a-b+$\sqrt{2}$-a+（b-$\sqrt{2}$）
=-3a-b+$\sqrt{2}$+b-$\sqrt{2}$
=-3a

點評 本題考查二次根式的性質，解題的關鍵是根據數軸判斷a、a+b、$\sqrt{2}$-a、b-$\sqrt{2}$與0的大小，本題屬于基礎題型．