【題目】已知
的半徑為
，弦
，
，
，則
、
之間的距離為________．
【答案】
或
．
【解析】
首先作AB、CD的垂線EF，然后根據垂徑定理求得CE=DE=10cm，AF=BF=24cm；再在直角三角形OED和直角三角形OBF中，利用勾股定理求得OE、OF的長度；最后根據圖示的兩種情況計算EF的長度即可．
有兩種情況.如圖.過O作AB、CD的垂線EF，交AB于點F，交CD于點E.
∴EF就是AB、CD間的距離。
∵AB=48cm，CD=20cm，根據垂徑定理，得CE=DE=10cm，AF=BF=24cm，
∵OD=OB=26cm，
∴在直角三角形OED和直角三角形OBF中，
∴OE=24cm，OF=10cm(勾股定理)，
∴①EF=24+10=34cm②EF=2410=14cm，
故答案為：34或14cm.
優質課堂快樂成長系列答案科目：初中數學 來源： 題型：
【題目】定義：幾個全等的正多邊形依次有一邊重合，排成一圈，中間可以圍成一個正多邊形，我們稱作正多邊形的環狀連接。如圖，我們可以看作正六邊形的環狀連接，中間圍成一個邊長相等的正六邊形；若正八邊形作環狀連接，中間可以圍的正多邊形的邊數為；
若正八邊形作環狀連接，中間可以圍的正多邊形的邊數為________，若邊長為1的正n邊形作環狀連接，中間圍成的是等邊三角形，則這個環狀連接的外輪廓長為_________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察與探究：
(1)觀察下列各組數據并填空：
A：1，2，3，4，5，
平均數xA＝________，方差sA2＝________；
B：11，12，13，14，15，
平均數xB＝________，方差sB2＝________；
C：10，20，30，40，50，
平均數xC＝________，方差sC2＝________；
(2)分別比較A與B，C的計算結果，你能發現什么規律？
查看答案和解析>>
科目：初中數學 來源： 題型：
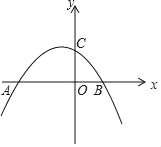
【題目】如圖，已知拋物線y=﹣
x2+bx+c與x軸交于點A（﹣4，0），B（2，0），與y軸交于點C．請解答下列問題：
（1）求拋物線的函數解析式并直接寫出頂點M坐標；
（2）連接AM，N是AM的中點，連接BN，求線段BN長．
注：拋物線y=ax2+bx+c（a≠0）的頂點坐標是（﹣
，
）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市為解決部分市民冬季集中取暖問題，需鋪設一條長4000米的管道，為盡量減少施工對交通造成的影響，施工時“…”，設實際每天鋪設管道x米，則可得方程
＝20，根據此情景，題中用“…”表示的缺失的條件應補為（ ）
A. 每天比原計劃多鋪設10米，結果延期20天完成
B. 每天比原計劃少鋪設10米，結果延期20天完成
C. 每天比原計劃多鋪設10米，結果提前20天完成
D. 每天比原計劃少鋪設10米，結果提前20天完成
查看答案和解析>>
科目：初中數學 來源： 題型：
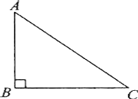
【題目】如圖，△ABC中，∠B＝90°，AB＝3，BC＝4，AC＝5；
實踐與操作：過點A作一條直線，使這條直線將△ABC分成面積相等的兩部分，直線與BC交于點D．（尺規作圖，不寫作法，保留作圖痕跡，標清字母）
推理與計算：求點D到AC的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線
上部分點的橫坐標
，縱坐標
的對應值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聰觀察上表，得出下面結論：①拋物線與軸的一個交點為
；②函數的最大值為
；③拋物線的對稱軸是
；④在對稱軸左側，隨增大而增大．其中正確有（ ）
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（觀察）
51×49＝（
）2﹣（
）2
102×98＝（
）2﹣（）2
2001×1999＝（
）2﹣（
）2
（發現）根據閱讀回答問題
（1）請根據上面式子的規律填空：
998×1002＝ 2﹣ 2
（2）在上述乘法運算中，設第一個因數為m，第二個因數為n，請用有m、n的符號語言寫出你所發現的規律，并證明．
（應用）請運用（發現）中總結的規律計算：59.8×60.2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
