
【題目】如果等式(x﹣3)2x﹣1=1,則x= .
【答案】![]() 或4
或4
【解析】解:①若2x﹣1=0, 解得x= ![]() ,
,
此時x﹣3=﹣2 ![]() ,
,
所以,x= ![]() 符合,
符合,
②若x﹣3=1,
解得x=4,
③若x﹣3=﹣1,
解得x=2,
此時2x﹣1=3,
所以,x=2符合,
綜上所述,x= ![]() 或4.
或4.
所以答案是: ![]() 或4.
或4.
【考點精析】關于本題考查的零指數冪法則和有理數的乘方,需要了解零次冪和負整數指數冪的意義: a0=1(a≠0);a-p=1/ap(a≠0,p為正整數);有理數乘方的法則:1、正數的任何次冪都是正數2、負數的奇次冪是負數;負數的偶次冪是正數;注意:當n為正奇數時: (-a)n=-an或(a -b)n=-(b-a)n , 當n為正偶數時: (-a)n =an 或 (a-b)n=(b-a)n才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】某校在踐行“社會主義核心價值觀”演講比賽中,對名列前20名的選手的綜合分數m進行分組統計,結果如表所示:

組號 | 分組 | 頻數 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形統計圖來描述,求分數在8≤m<9內所對應的扇形的圓心角的度數.
(3)將在第一組內的兩名選手記為A1,A2,在第四組內的兩名選手記為B1,B2, 從第一組和第四組中隨機選取2名選手進行調研座談,求第一組至少有1名選手被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校為了響應國家陽光體育活動,選派部分學生參加足球、乒乓球、籃球、排球隊集訓.根據參加項目制成如下兩幅不完整的統計圖(要求每位同學只能選擇一種自己喜歡的球類,圖中用足球、乒乓球、籃球、排球代表喜歡這四種球類某種球類的學生人數,請你根據圖中提供的信息解答下列問題:
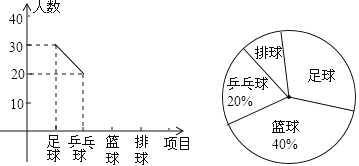
(1)參加籃球隊的有 人,參加足球隊的人數占全部參加人數的 %.
(2)喜歡排球隊的人數在扇形統計圖中所占的圓心角是多少度?并補全頻數分布折線統計圖.
(3)若足球隊只剩一個集訓名額,學生小明和小虎都想參加足球隊,決定采用隨機摸球的方式確定參加權,具體規則如下:一個不透明的袋子中裝著標有數字1、2、3、4的四個完全相同的小球,小明隨機地從四個小球中摸出一球然后放回,小虎再隨機地摸出一球,若小明摸出的小球標有數字比小虎摸出的小球標有的數字大,則小明參加;若小明摸出的小球標有數字比小虎摸出的小球標有的數字小,則小虎參加,試分析這種規則對雙方是否公平?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(a,0)、B(b,0),且(a+4)2+|b﹣2|=0. 
(1)求a、b的值.
(2)在y軸的正半軸上找一點C,使得三角形ABC的面積是15,求出點C的坐標.
(3)過(2)中的點C作直線MN∥x軸,在直線MN上是否存在點D,使得三角形ACD的面積是三角形ABC面積的 ![]() ?若存在,求出點D的坐標;若不存在,請說明理由.
?若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E、F分別在邊BC、CD上,且AE=EF=FA.下列結論:①△ABE≌△ADF;②CE=CF;③∠AEB=75°;④BE+DF=EF;⑤S△ABE+S△ADF=S△CEF , 其中正確的是①②③⑤(只填寫序號). 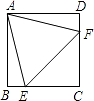
查看答案和解析>>
科目:初中數學 來源: 題型:
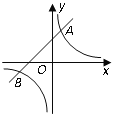
【題目】如圖,反比例函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點.
兩點.
(1)求反比例函數與一次函數的解析式;
(2)根據圖象回答:當![]() 取何值時,反比例函數的值大于一次函數的值.
取何值時,反比例函數的值大于一次函數的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() .
.
(1)若該反比例函數的圖象與直線![]() (
(![]() ≠0)只有一個公共點,求
≠0)只有一個公共點,求![]() 的值;
的值;
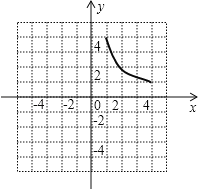
(2)如圖,反比例函數![]() 的圖象記為曲線
的圖象記為曲線![]() ,將
,將![]() 向左平移2個單位長度,得曲線
向左平移2個單位長度,得曲線![]() ,請在圖中畫出
,請在圖中畫出![]() ,并直接寫出
,并直接寫出![]() 平移至
平移至![]() 處 所掃過的面積.
處 所掃過的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com