
【題目】閱讀材料:
“三角形的三個頂點確定一個圓,這個圓叫做三角形的外接圓、外接圓的圓心叫做三角形的外心,這個三角形叫做這個圓的內接三角形。”(蘇科版《數學》九上 2.3確定圓的條件)
問題初探:
(1)三角形的外心到三角形的_____________距離相等
(2)若點O是△ABC的外心,試探索∠BOC與∠BAC之間的數量關系。
(3)如圖,在Rt△ABC中,∠ACB=90°,AC=BC。將線段BC繞點B逆時針旋轉30°到BD,連接AD、CD。用直尺和圓規在圖中作出△BCD的外心O,并求∠ADB的度數。(保留作圖痕跡,不寫作法。)
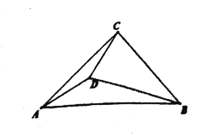
【答案】(1)三個頂點;(2)∠BOC=2∠BAC或∠BOC=360°-2∠BAC ;(3)![]()
【解析】
(1)由三角形的三頂點都在圓上且圓上個點到圓心的距離相等可得答案;
(2)分∠BAC為銳角、直角、鈍角三種情況,銳角時作直徑AD,由OA=OB=OC知∠OAB=∠OBA、∠OAC=∠OCA,據此得∠BOD=2∠BAO、∠COD=2∠CAO,根據∠BOC=∠BOD+∠COD可得;直角時由OA=OB=OC知點O是斜邊BC的中點,據此可得;鈍角時,根據∠BOC=∠BOA+∠COA=180°-∠BOD+180°-∠COD可得;
(3)由旋轉性質知BC=BD、∠BCD=∠BDC=75°,證△OCD為等邊三角形得OC=CD,再證△ACD≌△BCO得∠ADC=∠BOC=150°,根據∠ADB=360°-∠ADC-∠BDC可得答案.
解:(1)∵三角形的三頂點都在圓上,
∴圓心到三角形的三頂點的距離相等;
(2)①當∠BAC為銳角時,如圖1,作直徑AD,
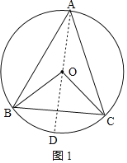
∵OA=OB=OC,
∴∠OAB=∠OBA、∠OAC=∠OCA,則∠BOD=2∠BAO,∠COD=2∠CAO,
∵∠BAC=∠BAO+∠CAO,
∴∠BOC=∠BOD+∠COD=2∠BAO+2∠CAO
=2(∠BAO+∠CAO)=2∠BAC;
②當∠BAC為直角時,如圖2,
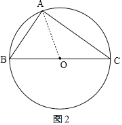
∵⊙O是△ABC的外接圓,
∴OA=OB=OC,
∴點O是斜邊BC的中點,此時∠BOC=180°,∠BAC=90°,
∴∠BOC=2∠BAC;
③當∠BAC為鈍角時,如圖3,作直徑AD,
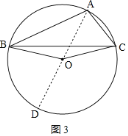
∵OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
則∠BOD=2∠BAO,∠COD=2∠CAO,
∵∠BAC=∠BAO+∠CAO,
∴∠BOC=∠BOA+∠COA=180°-∠BOD+180°-∠COD
=360°-(∠BOD+∠COD)=360°-(2∠BAO+2∠CAO)
=360°-2(∠BAO+∠CAO)=360°-2∠BAC,
即∠BOC=360°-2∠BAC;
綜上可知,∠BOC==2∠BAC或∠BOC=360°-2∠BAC;
(3)如圖4,點O為△BCD的外心,
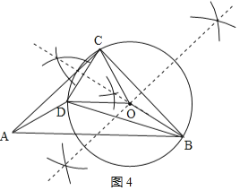
由“將線段BC繞點B逆時針方向旋轉30°到BD”可得:∠CBD=30°,CB=DB,
∴∠BCD=∠BDC=75°,
∴∠BOC=2∠BDC=150°.
又點O為△BCD的外心,
∴OB=OC,∠OBC=∠OCB=15°,
又∠ACD=∠ACB-∠BCD=15°,
∴∠ACD=∠BCO,∠OCD=60°,
∵OD=OC,
∴△OCD為等邊三角形,
∴CD=CO.
在△DCA和△OCB中,
∵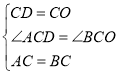 ,
,
∴△DCA≌△OCB(SAS),
∴∠ADC=∠BOC=150°,
∴∠ADB=360°-∠ADC-∠BDC=135°.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作⊙O交BC于點D.過點D作EF⊥AC,垂足為E,且交AB的延長線于點F.
(1)求證:EF是⊙O的切線;(2)若AB=8,∠A=60°,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
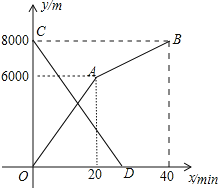
【題目】小明和小亮分別從甲地和乙地同時出發,沿同一條路相向而行,小明開始跑步,中途改為步行,到達乙地恰好用![]() 小亮騎自行車以
小亮騎自行車以![]() 的速度直接到甲地,兩人離甲地的路程
的速度直接到甲地,兩人離甲地的路程![]() 與各自離開出發地的時間
與各自離開出發地的時間![]() 之間的函數圖象如圖所示,
之間的函數圖象如圖所示,
![]() 甲、乙兩地之間的路程為______m,小明步行的速度為______
甲、乙兩地之間的路程為______m,小明步行的速度為______![]() ;
;
![]() 求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
![]() 求兩人相遇的時間.
求兩人相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的布袋里裝有4個大小、質地均相同的乒乓球,每個球上面分別標有1,2,3,4.小林先從布袋中隨機抽取一個乒乓球(不放回去),再從剩下的3個球中隨機抽取第二個乒乓球,記兩次取得乒乓球上的數字依次為a、b.
(1)求a、b之積為偶數的概率;
(2)若c=5,求長為a、b、c的三條線段能圍成三角形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,且AB=AC,點D在弧BC上運動,過點D作DE∥BC,DE交AB的延長線于點E,連接AD、BD。

(1)求證:∠ADB=∠E;
(2)當AB=5,BC=6時,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=-x+4與x軸交于A點,與y軸交于B點,動點P從A點出發,以每秒2個單位的速度沿AO方向向點O勻速運動,點E是點B以Q為對稱中心的對稱點,同時動點Q從B點出發,以每秒1個單位的速度沿BA方向向點A勻速運動,當一個點停止運動,另一個點也隨之停止運動,連結PQ,設P,Q兩點運動時間為t秒(0<t≤2).

(1)直接寫出A,B兩點的坐標.
(2)當t為何值時,PQ∥OB?
(3)四邊形PQBO面積能否是△ABO面積的![]() ;若能,求出此時t的值;若不能,請說明理由;
;若能,求出此時t的值;若不能,請說明理由;
(4)當t為何值時,△APE為直角三角形?(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】高爾夫運動員將一個小球沿與地面成一定角度的方向擊出,在不考慮空氣阻力的條件下,小球的飛行高度h(m)與它的飛行時間(s)滿足二次函數關系,t與h的幾組對應值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h與t之間的函數關系式(不要求寫t的取值范圍);
(2)求小球飛行3s時的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知x1,x2是一元二次方程4kx2-4kx+k+1=0的兩個實數根.
(1)是否存在實數k,使(2x1-x2)(x1-2x2)=-![]() 成立?若存在,求出k的值;若不存在,請說明理由;
成立?若存在,求出k的值;若不存在,請說明理由;
(2)求使![]() -2的值為整數的整數k的值.
-2的值為整數的整數k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知第一象限內的點A在反比例函數y=![]() 的圖象上,第二象限內的點B在反比例函數y=
的圖象上,第二象限內的點B在反比例函數y=![]() 的圖象上,且OA⊥OB,cosA=
的圖象上,且OA⊥OB,cosA=![]() ,則k的值為( )
,則k的值為( )

A. -3 B. -6 C. -4 D. -![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com