
如圖,矩形OABC的頂點A在y軸上,C在x軸上,雙曲線y=
 與AB交于點D,與BC交于點E,DF⊥x軸于點F,EG⊥y軸于點G,交DF于點H.若矩形OGHF和矩形HDBE的面積分別是1和2,則k的值為( )
與AB交于點D,與BC交于點E,DF⊥x軸于點F,EG⊥y軸于點G,交DF于點H.若矩形OGHF和矩形HDBE的面積分別是1和2,則k的值為( )


A.
 B.
B.
 +1 C.
+1 C.
 D.2
D.2

B【考點】反比例函數系數k的幾何意義.
【專題】計算題.
【分析】設D(t,
 ),由矩形OGHF的面積為1得到HF=
),由矩形OGHF的面積為1得到HF=
 ,于是根據反比例函數圖象上點的坐標特征可表示出E點坐標為(kt,
,于是根據反比例函數圖象上點的坐標特征可表示出E點坐標為(kt,
 ),接著利用矩形面積公式得到(kt﹣t)•(
),接著利用矩形面積公式得到(kt﹣t)•(
 ﹣
﹣
 )=2,然后解關于k的方程即可得到滿足條件的k的值.
)=2,然后解關于k的方程即可得到滿足條件的k的值.
【解答】解:設D(t,
 ),
),
∵矩形OGHF的面積為1,DF⊥x軸于點F,
∴HF=
 ,
,
而EG⊥y軸于點G,
∴E點的縱坐標為
 ,
,
當y=
 時,
時,
 =
=
 ,解得x=kt,
,解得x=kt,
∴E(kt,
 ),
),
∵矩形HDBE的面積為2,
∴(kt﹣t)•(
 ﹣
﹣
 )=2,
)=2,
整理得(k﹣1)2=2,
而k>0,
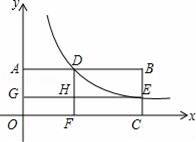
∴k=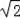
 +1.
+1.
故選B.

【點評】本題考查了反比例函數比例系數k的幾何意義:在反比例函數y=
 圖象中任取一點,過這一個點向x軸和y軸分別作垂線,與坐標軸圍成的矩形的面積是定值|k|.
圖象中任取一點,過這一個點向x軸和y軸分別作垂線,與坐標軸圍成的矩形的面積是定值|k|.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
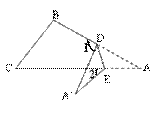
如圖,把△ABC紙片沿DE折疊,當點A落在四邊形BCDE的外部時,則 與
與 和
和 之間有一種數量關系始終保持不變,請試著找一找這個規律,你發現的規律是( )
之間有一種數量關系始終保持不變,請試著找一找這個規律,你發現的規律是( )
A. B.
B.
C. D.
D.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,四個幾何體分別為長方體、圓柱體、球體和三棱柱,這四個幾何體中有三個的某一種視圖都是同一種幾何圖形,則另一個幾何體是( )
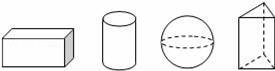

A.長方體 B.圓柱體 C.球體 D.三棱柱
查看答案和解析>>
科目:初中數學 來源: 題型:
對于函數y= - ,下列結論錯誤的是 ( )
,下列結論錯誤的是 ( )
A、當x>0時,y隨x的增大而增大
B、當x<0時,y隨x的增大而增大
C、當x=1時的函數值大于x= -1時的函數值
D、在函數圖象所在的象限內,y隨x的增大而增大
查看答案和解析>>
科目:初中數學 來源: 題型:
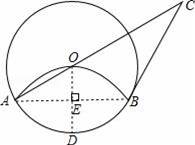
如圖,將圓形紙片沿弦AB折疊后,圓弧恰好能經過圓心O,⊙O的切線BC與AO延長線交于點C.
(1)若⊙O半徑為6cm,用扇形OAB圍成一個圓錐的側面,求這個圓錐的底面圓半徑.
(2)求證:AB=BC.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com