
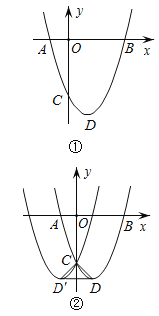
【題目】如圖①,在平面直角坐標系中,拋物線![]() (
(![]() )與x軸相交于A,B兩點,與y軸相交于點C,頂點為D.
)與x軸相交于A,B兩點,與y軸相交于點C,頂點為D.
(1)當a=1時,拋物線頂點D的坐標為________,AB=_________;
(2)AB的長是否與a有關?說明你的理由;
(3)若將拋物線![]() (
(![]() )沿y軸折疊,得到另一拋物線,其頂點為D,如圖②.連接CD,CD和DD.
)沿y軸折疊,得到另一拋物線,其頂點為D,如圖②.連接CD,CD和DD.
①若△CDD為等邊三角形時,則a=______;
②若△CDD為等腰直角三角形時,則a=______.
【答案】(1)(1,-4),4;(2)AB的長與a無關,見解析;(3)①![]() ; ② 1
; ② 1
【解析】
(1)將a=1代入解析式,并將解析式變形為頂點式,得到頂點坐標;另y=0得到點A、B的坐標;
(2)A、B是拋物線與x軸的交點,先求解出A、B兩點的坐標,根據坐標求解距離,看計算得出的結果中是否含有字母a;
(3)①求解出點C、D、D的坐標(用a表示),利用等邊三角形三邊相等的性質求解a;
②同上,先得出坐標點,利用勾股股定理的逆定理列寫等式求解a
(1)將a=1代入解析式得:![]()
變形為頂點式為:![]()
∴頂點坐標為:(1,-4)
另y=0得:![]()
解得:x=-1或x=3
設點A在點B的左側
∴A(-1,0),B(3,0)
∴AB=4
(2)AB的長與a無關
理由是:當y=0時,
![]() .
.
解得![]() ,
,![]() .
.
∴A(-1,0),B(3,0).
∴AB=3-(-1)= 4.
∴AB的長與a無關
(3)①拋物線![]()
點C為與y軸的交點,即x=0
得:y=-3a,∴C(0,-3a)
將拋物線變形為頂點式為:![]()
故頂點D(1,-4a)
∵D與點D關于y軸對稱
∴D(-1,4a)
∴DD=2,CD=![]()
∵△CDD是等邊三角形
∴DD=CD,即2=![]()
解得:a=![]()
②∵CD=CD,∴△CDD肯定是等腰三角形
∵△CDD是等腰直角三角形
∴![]() ,即:
,即:![]()
解得:a=1


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:①abc>0;②2a+b=0;③若m為任意實數,則a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2.其中,正確結論的個數為( )
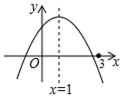
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】北京地鐵票價計費標準如下表所示:
乘車距離 |
|
|
|
|
|
票價(元) | 3 | 4 | 5 | 6 | 每增加1元可乘坐20公里 |
另外,使用市政交通一卡通,每個自然月每張卡片支出累計滿100元后,超出部分打8折;滿150元后,超出部分打5折;支出累計達400元后,不再打折.小紅媽媽上班時,需要乘坐地鐵15公里到達公司,每天上下班共乘坐兩次.如果每次乘坐地鐵都使用市政交通一卡通,那么每月第21次乘坐地鐵上下班時,她刷卡支出的費用( )
A.2.5元B.3元C.4元D.5元
查看答案和解析>>
科目:初中數學 來源: 題型:
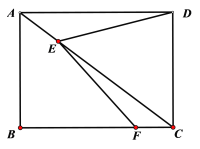
【題目】如圖,矩形ABCD的對角線上有動點E,連結DE,邊BC上有一定點F,連接EF,已知AB=3cm,AD=4cm,設A,E兩點間的距離為![]() cm,D,E兩點間的距離為
cm,D,E兩點間的距離為![]() cm,E,F兩點間的距離為
cm,E,F兩點間的距離為![]() cm.
cm.
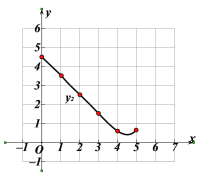
小勝根據學習函數的經驗,分別對函數![]() ,
,![]() 隨自變量x的變化而變化的規律進行了探究.下面是小勝的探究過程,請補充完整:
隨自變量x的變化而變化的規律進行了探究.下面是小勝的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,得到x與y的幾組對應值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
(2)在同一平面直角坐標系xOy中,描出補全后的表中各組數值所對應的點![]() ,并畫出函數
,并畫出函數![]() 的圖像:
的圖像:
(3)結合函數圖像,解決問題:當DE>EF時,AE的長度范圍約為_________________cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
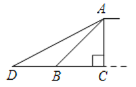
【題目】某市為了緩解城市交通壓力,決定修建人行天橋,原設計天橋的樓梯與地面的夾角為45°(∠ABC=45°),BC=4.2 m,后考慮安全因素,將樓梯角B移到CB的延長線上點D處,使∠ADC=23°(如圖所示).求BD的長(精確到0.1 m).(參考數據:sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國內豬肉價格不斷上漲,已知今年10月的豬肉價格比今年年初上漲了80%,李奶奶10月在某超市購買1千克豬肉花了72元錢.
(1)今年年初豬肉的價格為每千克多少元?
(2)某超市將進貨價為每千克55元的豬肉按10月價格出售,平均一天能銷售出100千克,隨著國家對豬肉價格的調控,超市發現豬肉的售價每千克下降1元,其日銷售量就增加10千克,超市為了實現銷售豬肉每天有1800元的利潤,并且盡可能讓顧客得到實惠,豬肉的售價應該下降多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
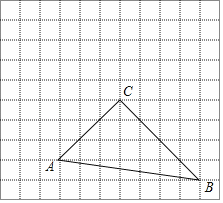
【題目】如圖,在每個小正方形的邊長為1的網格中,△ABC的頂點A、B、C均在格點上.
(1)∠ACB的大小為 ;
(2)在如圖所示的網格中以A為中心,取旋轉角等于∠BAC,把△ABC逆時針旋轉,請用無刻度的直尺,畫出旋轉后的△AB'C',保留作圖痕跡,不要求證明;
(3)點P是BC邊上任意一點,在(2)的旋轉過程中,點P的對應點為P',當線段CP'最短時,CP'的長度為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC中,∠A=30°,點P從點A出發以2cm/s的速度沿折線A→C→B運動,點Q從點A出發以vcm/s的速度沿AB運動,P,Q兩點同時出發,當某一點運動到點B時,兩點同時停止運動.設運動時間為x(s),△APQ的面積為y(cm2),y關于x的函數圖象由C1,C2兩段組成,如圖2所示,有下列結論:①v=1;②sinB=![]() ;③圖象C2段的函數表達式為y=﹣
;③圖象C2段的函數表達式為y=﹣![]() x2+
x2+![]() x;④△APQ面積的最大值為8,其中正確有( )
x;④△APQ面積的最大值為8,其中正確有( )
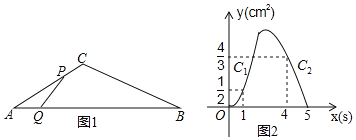
A.①②B.①②④C.①③④D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com