
【題目】如圖,正方形ABCD中,點E是AD邊的中點,BD、CE交于點H,BE、AH交于點G,則下列結論:①AG⊥BE;②BE:BC=![]() :2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正確的個數是
:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正確的個數是

A.1B.2C.3D.4
【答案】D
【解析】
首先根據正方形的性質證得△BAE≌△CDE,推出∠ABE=∠DCE,再證 △ADH≌△CDH,求得∠HAD=∠HCD,推出∠ABE=∠HAD:求出∠ABE+∠BAG=90°;最后在△AGE中根據三角形的內角和是180°求得∠AGE=90°即可得到①正確;
因為點E是AD邊的中點,求出AB= 2AE,BE=![]() AE
AE
即可求得BE:BC=![]() :2,故②正確;
:2,故②正確;
根據 AD ∥BC,求出S△BDE=S△CDE,推出 S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,故③正確;
由∠AHD=∠CHD,得到鄰補角和對頂角相等得到∠AHB=∠EHD,故④正確
∵四邊形ABCD是正方形,E是AD邊上的中點,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
在△BAE和△CDE中
∵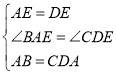
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
∵四邊形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,
∵在△ADH和△CDH中,
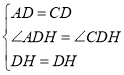
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°-90°=90°,
∴AG⊥BE,故①正確;
∵點E是AD邊的中點,
∴AB= 2AE,
∴BE=![]() AE
AE
∴BE:BC=![]() :2,故②正確;
:2,故②正確;
∵AD∥BC,∴S△BDE=S△CDE,
∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,故③正確;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,故④正確;
故選:D.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊),與
的左邊),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() .
.
![]() 求
求![]() 、
、![]() 、
、![]() 三點的坐標及拋物線的對稱軸;
三點的坐標及拋物線的對稱軸;
![]() 若已知
若已知![]() 軸上一點
軸上一點![]() ,則在拋物線的對稱軸上是否存在一點
,則在拋物線的對稱軸上是否存在一點![]() ,使得
,使得![]() 是直角三角形?若存在,求出點
是直角三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在20km越野賽中,甲乙兩選手的行程y(單位:km)隨時間 x(單位:h)變化的圖象如圖所示,

根據圖中提供的信息,有下列說法:①兩人相遇前,甲的速度小于乙的速度;②出發后1小時,兩人行程均為10km;③出發后1.5小時,甲的行程比乙多3km;④甲比乙先到達終點.其中正確的有____個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場用5500元購進甲、乙兩種礦泉水共180箱,礦泉水的成本價與銷售價如下表所示:
類別 | 成本價(元 | 銷售價(元 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)購進甲、乙兩種礦泉水各多少箱?
(2)該商場售完這180箱礦泉水,可獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
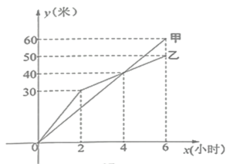
【題目】浦東新區在創建文明城區的活動中,有兩段長度相等的彩色道磚路面的鋪設任務,分別交給甲、乙兩個施工隊同時進行施工.如圖是反映所鋪設的彩色道磚路面的長度![]() (米)與施工時間
(米)與施工時間![]() (時)之間關系的部分圖像.請根據題意回答下列問題:
(時)之間關系的部分圖像.請根據題意回答下列問題:
(1)甲隊每小時施工_________米;
(2)乙隊在![]() 時段內,
時段內,![]() 與
與![]() 之間的函數關系式是_________;
之間的函數關系式是_________;
(3)在![]() 時段內,甲隊比乙隊每小時快_________米;
時段內,甲隊比乙隊每小時快_________米;
(4)如果甲隊施工速度不變,乙隊在![]() 小時后,施工速度增加到
小時后,施工速度增加到![]() 米/時,結果兩隊同時完成了任務.則甲隊從開始施工到完工所鋪設的彩色道磚路面的長度為_________米.
米/時,結果兩隊同時完成了任務.則甲隊從開始施工到完工所鋪設的彩色道磚路面的長度為_________米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣(x﹣1)2+c與x軸交于A,B(A,B分別在y軸的左右兩側)兩點,與y軸的正半軸交于點C,頂點為D,已知A(﹣1,0).
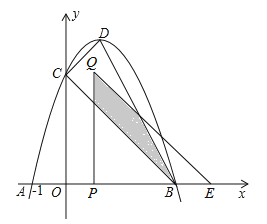
(1)求點B,C的坐標;
(2)判斷△CDB的形狀并說明理由;
(3)將△COB沿x軸向右平移t個單位長度(0<t<3)得到△QPE.△QPE與△CDB重疊部分(如圖中陰影部分)面積為S,求S與t的函數關系式,并寫出自變量t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com