
【題目】已知拋物線y=ax2+bx+c過點A(0,2)。
(1)若點(-![]() ,0)也在該拋物線上,求a,b滿足的關系式;
,0)也在該拋物線上,求a,b滿足的關系式;
(2)若點A為拋物線頂點,且拋物線過點(1,1)。
①求拋物線的解析式;
②若點M是拋物線上異于點A的一個動點,點P與點O關于點A對稱,直線MP交拋物線與另一個點N,點N’是拋物線上點N關于對稱軸的對稱點,直線PN’與拋物線交于點E,求證:直線EN恒過點O。
【答案】(1)3a-![]() b=-2;(2)①y=-
b=-2;(2)①y=-![]() +2,②見解析
+2,②見解析
【解析】
(1)由拋物線經過點A可求出c=2,再代入(-![]() ,0)即可找出3a-
,0)即可找出3a-![]() b=-2(a≠0);
b=-2(a≠0);
(2)由A點為拋物線的頂點,可設y=ax2+2,把(1,1)代入求出a的值即可;
(3)設M點的坐標為(m,m2+2)求出直線PM的解析式,與拋物線方程聯立,求出N點坐標,根據M點與E點關于y軸對稱求出E點坐標,從而求出直線EN的解析式,判斷當x=0時,y=0即可.
(1)∵拋物線y=ax2+bx+c過點A(0,2),
∴c=2.
又∵點(-![]() ,0)也在該拋物線上,
,0)也在該拋物線上,
∴a(-![]() )2+b(-
)2+b(-![]() )+c=0,
)+c=0,
∴3a-![]() b+2=0(a≠0).
b+2=0(a≠0).
即3a-![]() b=-2;
b=-2;
(2)∵點A(0,2)是拋物線的頂點坐標,
∴設![]() ,
,
∵函數![]() 的圖象經過(1,1)
的圖象經過(1,1)
∴1=a+2,解得,a=-1,
∴拋物線的解析式為:![]()
(3)設M點的坐標為(m,-m2+2)(m<0),
設直線PM的解析式為:![]()
∵點P與點O關于點A對稱,A(0,2),
∴P(0,4),

∴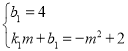 ,
,
解得,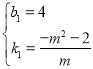 ,
,
∴直線PM的解析式為:![]() ,
,
聯立方程組得,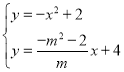
解得, ,
, ,
,
∴N(![]() ,
,![]() ).
).
∵M點與E點關于y軸對稱,
∴E(-m,-m2+2)
設直線NE的解析式為:![]() ,
,
將N點、E點坐標代入得,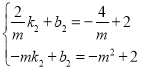 ,解得,
,解得,
∴直線EN的解析式為:![]()
∴當x=0時,y=0,
∴直線EN恒過點O.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】已知正方形ABCD中,AB=6,點P是射線BC上的一動點,過點P作PE⊥PA交直線CD于E,連AE.

(1)如圖1,若BP=2,求DE的長;
(2)如圖2,若AP平分∠BAE,連PD,求tan∠DPE的值;
(3)直線PD,AE交于點F,若BC=4PC,則![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() .
.
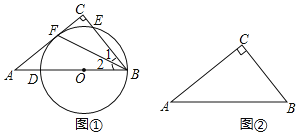
(1)如圖①,點![]() 在斜邊
在斜邊![]() 上,以點
上,以點![]() 為圓心,
為圓心,![]() 長為半徑的圓交
長為半徑的圓交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,與邊
,與邊![]() 相切于點
相切于點![]() .求證:
.求證:![]() ;
;
(2)在圖②中作![]() ,使它滿足以下條件:
,使它滿足以下條件:
①圓心在邊![]() 上;②經過點
上;②經過點![]() ;③與邊
;③與邊![]() 相切.
相切.
(尺規作圖,只保留作圖痕跡,不要求寫出作法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,過原點O及點A(8,0),C(0,6)作矩形OABC、連結OB,點D為OB的中點,點E是線段AB上的動點,連結DE,作DF⊥DE,交OA于點F,連結EF.已知點E從A點出發,以每秒1個單位長度的速度在線段AB上移動,設移動時間為t秒.

(1)如圖1,當t=3時,求DF的長.
(2)如圖2,當點E在線段AB上移動的過程中,∠DEF的大小是否發生變化?如果變化,請說明理由;如果不變,請求出tan∠DEF的值.
(3)連結AD,當AD將△DEF分成的兩部分的面積之比為1:2時,求相應的t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB為直徑,AC=5,AB=10,
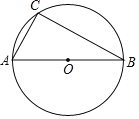
(1)作以AC為底邊的圓內接等腰△ACD;(要求:尺規作圖,不寫作法,保留作圖痕跡)
(2)求弦AC所對的圓周角。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在同一平面內,將兩個全等的等腰直角三角形![]() 和
和![]() 擺放在一起,
擺放在一起,![]() 為公共頂點,
為公共頂點,![]() ,若
,若![]() 固定不動,
固定不動,![]() 繞點
繞點![]() 旋轉,
旋轉,![]() 、
、![]() 與邊
與邊![]() 的交點分別為
的交點分別為![]() 、
、![]() (點
(點![]() 不與點
不與點![]() 重合,點
重合,點![]() 不與點
不與點![]() 重合).
重合).
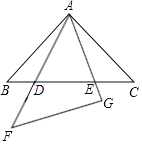
(1)求證:![]() ;
;
(2)在旋轉過程中,試判斷等式![]() 是否始終成立,若成立,請證明;若不成立,請說明理由.
是否始終成立,若成立,請證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() (
(![]() ,
,![]() ,
,![]() 為常數,且
為常數,且![]() )中的
)中的![]() 與
與![]() 的部分對應值如下表:
的部分對應值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下結論:
①二次函數![]() 有最小值為
有最小值為![]() ;
;
②當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
③二次函數![]() 的圖象與
的圖象與![]() 軸只有一個交點;
軸只有一個交點;
④當![]() 時,
時,![]() .
.
其中正確的結論有( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四張反面完全相同的紙牌![]() ,其正面分別畫有四個不同的幾何圖形,將四張紙牌洗勻正面朝下隨機放在桌面上.
,其正面分別畫有四個不同的幾何圖形,將四張紙牌洗勻正面朝下隨機放在桌面上.
(1)從四張紙牌中隨機摸出一張,摸出的牌面圖形是中心對稱圖形的概率是 .
(2)小明和小亮約定做一個游戲,其規則為:先由小明隨機摸出一張,不放回.再由小亮從剩下的紙牌中隨機摸出一張,若摸出的兩張牌面圖形既是軸對稱圖形又是中心對稱圖形,則小亮獲勝,否則小明獲勝.這個游戲公平嗎?請用列表法(或畫樹狀圖)說明理由.(紙牌用![]() 表示)若不公平,請你幫忙修改一下游戲規則,使游戲公平.
表示)若不公平,請你幫忙修改一下游戲規則,使游戲公平.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第 24 屆冬奧會將于 2022 年在北京和張家口舉行,冬奧會的項目有滑雪(如跳臺滑雪、高山滑雪、單板滑雪等)、滑冰(如短道速滑、速度滑冰、花樣滑冰等)、冰球、冰壺等.如圖,有 5 張形狀、大小、質地均相同的卡片,正面分別印有高山滑雪、速度滑冰、冰球、單板滑雪、冰壺五種不同的圖案,背面完全相同.現將這 5 張卡片洗勻后正面向下放在桌子上,從中隨機抽取一張,抽出的卡片正面恰好是滑雪項目圖案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com