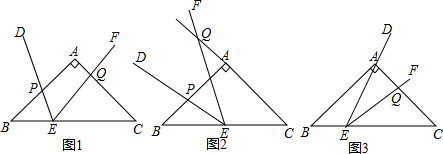
等腰直角△ABC中,∠ACB=90°,點D和E在AB邊上,AD=3,BE=4,∠DCE=45°,則DE= 或 .
【答案】
分析:根據題意畫出圖形,分兩種情況討論.根據∠DCE=∠CAE=∠DBC=45°判斷出△ACE∽△CDE∽△BDC,利用相似三角形的性質列出比例式,由比例式得到關于x的方程,解方程可得到DE的長.
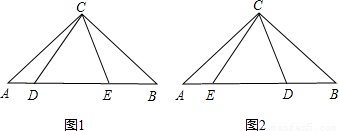
解答:解:如圖1:設DE=x,則AB=7+x,
∵∠DCE=∠CAE=∠DBC=45°
∴△ACE∽△CDE∽△BDC,
設CD=a,CE=b,
則有以下等式:
x:b=b:3+x,
x:a=a:4+x,
x:a=b:AC,
整理得,b
2=x(x+3),
a
2=x(x+4),
x•AC=ab,
x
2(x+3)(x+4)=a
2b
2=x
2•AC
2=
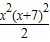
,
解得,x=5;
如圖2:與(1)類似,
得12x
2=a
2b
2=
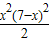
,
x=7-2
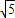
或x=7+2
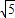
>7(舍去),
∴x=5或x=7-2
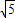
.
 點評:
點評:本題考查了等腰直角三角形,根據角的值證出三角形相似并建立關于ED的方程是解題的關鍵.

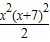 ,
,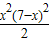 ,
,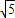 或x=7+2
或x=7+2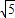 >7(舍去),
>7(舍去),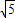 .
.