
【題目】如圖1,直線![]() 分別交x軸、y軸于A、B兩點,點P是線段AB上的一動點,以P為圓心,r為半徑畫圓.
分別交x軸、y軸于A、B兩點,點P是線段AB上的一動點,以P為圓心,r為半徑畫圓.
(1)若點P的橫坐標為﹣3,當⊙P與x軸相切時,則半徑r為 ,此時⊙P與y軸的位置關系是 .(直接寫結果)
(2)若![]() ,當⊙P與坐標軸有且只有3個公共點時,求點P的坐標.
,當⊙P與坐標軸有且只有3個公共點時,求點P的坐標.
(3)如圖2,當圓心P與A重合,![]() 時,設點C為⊙P上的一個動點,連接OC,將線段OC繞點O順時針旋轉90°,得到線段OD,連接AD,求AD長的最值并直接寫出對應的點D的坐標.
時,設點C為⊙P上的一個動點,連接OC,將線段OC繞點O順時針旋轉90°,得到線段OD,連接AD,求AD長的最值并直接寫出對應的點D的坐標.


【答案】(1)![]() ,相離,(2)P
,相離,(2)P![]() 或P
或P![]() ;(3)當點D在線段AB上時,AD最小值為
;(3)當點D在線段AB上時,AD最小值為![]() ,點D坐標為
,點D坐標為![]() ,當點D在線段AB的延長線上時,AD最大值為
,當點D在線段AB的延長線上時,AD最大值為![]() ,點D坐標為
,點D坐標為![]()
【解析】
(1)根據坐標軸上點的坐標特征求出A點和B點的坐標,根據相似三角形的性質解答;
(2)根據直線與圓的位置關系解答;
(3)連接AC,BD,證明△AOC≌△BOD,求出BD的長,得到AD最長或最短距離,根據直角三角形的性質求出點D的坐標.
(1)當x=0時,y=4, 當y=0時,x=-4,
∴A點的坐標為(-4,0),B點的坐標為(0,4),
點N為⊙P與x軸的切點,連接PN,
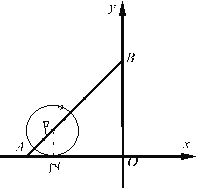
則PN∥OB,
∴![]() ,即
,即![]() ,
,
解得,PN=1,
x+4=1,
解得,x=3,
∵3>1,
∴⊙P與y軸的位置關系是相離,
故答案為:1;相離;
(2)當r=![]() ,⊙P與x軸相切時,
,⊙P與x軸相切時,
由![]() =x+4,得x=
=x+4,得x=![]() ,
,
則⊙P與y軸相交,
此時點P的坐標為(![]() ,
,![]() ),
),
當r=![]() ,⊙P與y軸相切時,
,⊙P與y軸相切時,
由y=![]() +4=
+4=![]() ,
,
則P與x軸相交,
此時點P的坐標為(-![]() ,
,![]() );
);
(3)連接AC、BD,

∵∠COD=∠AOB=90°
∴∠COA=∠DOB
易證△AOC≌△BOD
∴BD=AC=2
∴點D的運動軌跡是以點B為圓心,2為半徑的圓,
當點D在線段AB上時,AD最小值為![]() ,點D坐標為
,點D坐標為![]() ;
;
當點D在線段AB的延長線上時,AD最大值為![]() ,點D坐標為
,點D坐標為![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,分別以線段AC的兩個端點A,C為圓心,大于![]() AC的長為半徑畫弧,兩弧相交于B,D兩點,連接BD,AB,BC,CD,DA,以下結論:
AC的長為半徑畫弧,兩弧相交于B,D兩點,連接BD,AB,BC,CD,DA,以下結論:
①BD垂直平分AC;
②AC平分∠BAD;
③AC=BD;
④四邊形ABCD是中心對稱圖形.
其中正確的有( )
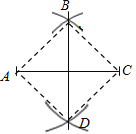
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一組數,按照下列規律排列:
1,
2,3,
6,5,4,
7,8,9,10,
15,14,13,12,11,
16,17,18,19,20,21,
……
數字5在第三行左數第二個,我們用(3,2)點示5的位置,那點這組成數里的數字100的位置可以表示為( )
A. (14,9) B. (14,10) C. (14,11) D. (14,12)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,由12個形狀、大小完全相同的小矩形組成一個大的矩形網格,小矩形的頂點稱為這個矩形網格的格點,已知這個大矩形網格的寬為4,△ABC的頂點都在格點.
(1)求每個小矩形的長與寬;
(2)在矩形網格中找出所有的格點E,使△ABE為直角三角形;(描出相應的點,并分別用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實施課程改革,為初三學生設置了A,B,C,D,E,F共六門不同的拓展性課程,現隨機抽取若干學生進行了“我最想選的一門課”調查,并將調查結果繪制成如圖統計圖表(不完整)
選修課 | A | B | C | D | E | F |
人數 | 20 | 30 |
根據圖標提供的信息,下列結論錯誤的是( )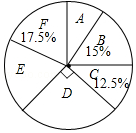
A.這次被調查的學生人數為200人
B.扇形統計圖中E部分扇形的圓心角為72°
C.被調查的學生中最想選F的人數為35人
D.被調查的學生中最想選D的有55人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的兩條高線BD,CE相交于點F,已知∠ABC=60°,AB=10,CF=EF,則△ABC的面積為( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,由12個形狀、大小完全相同的小矩形組成一個大的矩形網格,小矩形的頂點稱為這個矩形網格的格點,已知這個大矩形網格的寬為4,△ABC的頂點都在格點.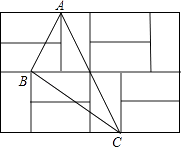
(1)求每個小矩形的長與寬;
(2)在矩形網格中找出所有的格點E,使△ABE為直角三角形;(描出相應的點,并分別用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,⊙A切y軸于點B,且點A在反比例函數y= ![]() (x>0)的圖象上,連接OA交⊙A于點C,且點C為OA中點,則圖中陰影部分的面積為( )
(x>0)的圖象上,連接OA交⊙A于點C,且點C為OA中點,則圖中陰影部分的面積為( ) 
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com