Question

試證明：二次函數y=nx²-2mx-2n的圖象與x軸交于不同的A、B兩點，并回答下列問題：
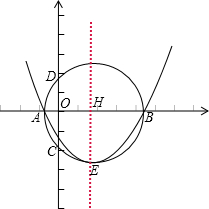
若二次函數y=nx²-2mx-2n的圖象的頂點在以AB為直徑的圓上．
（1）m、n間有何關系？
（2）設以AB為直徑的圓與y軸交于點C、D，弦CD的長是否為定值？

Answer 1

分析：（1）要證明原拋物線與x軸有兩個不同的交點，只要證明當y=0時△＞0就可以說明拋物線與x軸有兩個不同的交點．然后將拋物線的解析式轉化為頂點式，再根據根與系數的關系和兩點間的距離公式可以求出m、n之間的數量關系．
（2）利用垂徑定理和圓周角定理可以證明三角形相似來證明OD²=AO•OB，根據根與系數的關系可以求出OD的值，從而求出CD的值，判斷其為定值．

解答：解：令y=0時，則nx²-2mx-2n=0，
∴△=（-2m）²-4n（-2n）
=4m²+8n²
∵n≠0
∴△＞0
∴方程nx²-2mx-2n=0有兩個不同的實數根x₁，x₂
∴二次函數y=nx²-2mx-2n的圖象與x軸交于不同的交點．
（1）∵y=nx²-2mx-2n
∴y=（x-

m

n

）²-2n-

m2

n

所以它的頂點坐標為（

m

n

，-2n-

m2

n

）
HE=|-2n-

m2

n

|
∵x₁+x₂=

2m

n

，x₁•x₂=-2
∴AB=|x₁-x₂|=

(x1-x2) 2

=

(x1+x2)2-4x1x2

=

4m2 n2 +8

∴

4m2 n2 +8

=2|-2n-

m2

n

|
變形為：m²+2n²=1

（2）連接AD、BD
∴∠ADB=90°
∴OD²=OA•OB=|x₁|•|x₂|=|x₁x₂|=2
∴OD=

2

∵CD=2OD
∴CD=2

2

即CD的長為恒值2

2

．

點評：本題是一道二次函數的綜合題，考查了二次函數的圖象與x軸的交點坐標情況，根與系數的關系及頂點坐標的運用以及定長的問題．