
如圖,在平面直角坐標系中,頂點為(4,﹣1)的拋物線交y軸于A點,交x軸于B,C兩點(點B在點C的左側),已知A點坐標為(0,3).
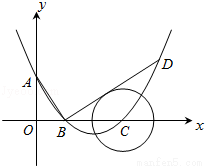
(1)求此拋物線的解析式
(2)過點B作線段AB的垂線交拋物線于點D,如果以點C為圓心的圓與直線BD相切,請判斷拋物線的對稱軸l與⊙C有怎樣的位置關系,并給出證明;
(3)已知點P是拋物線上的一個動點,且位于A,C兩點之間,問:當點P運動到什么位置時,△PAC的面積最大?并求出此時P點的坐標和△PAC的最大面積.
(1)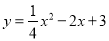 ;(2)相交.證明見解析;(3)當m=3時,△PAC的面積最大為
;(2)相交.證明見解析;(3)當m=3時,△PAC的面積最大為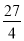 ;此時,P點的坐標為(3,-
;此時,P點的坐標為(3,-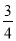 ).
).
【解析】
試題分析:(1)已知拋物線的頂點坐標,可用頂點式設拋物線的解析式,然后將A點坐標代入其中,即可求出此二次函數的解析式;
(2)根據拋物線的解析式,易求得對稱軸l的解析式及B、C的坐標,分別求出直線AB、BD、CE的解析式,再求出CE的長,與到拋物線的對稱軸的距離相比較即可;
(3)過P作y軸的平行線,交AC于Q;易求得直線AC的解析式,可設出P點的坐標,進而可表示出P、Q的縱坐標,也就得出了PQ的長;然后根據三角形面積的計算方法,可得出關于△PAC的面積與P點橫坐標的函數關系式,根據所得函數的性質即可求出△PAC的最大面積及對應的P點坐標.
試題解析:(1)設拋物線為y=a(x﹣4)2﹣1,
∵拋物線經過點A(0,3),
∴3=a(0﹣4)2﹣1,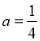 ;
;
∴拋物線為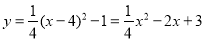
(2)相交.
證明:連接CE,則CE⊥BD,
當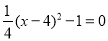 時,x1=2,x2=6.
時,x1=2,x2=6.
A(0,3),B(2,0),C(6,0),
對稱軸x=4,
∴OB=2,AB=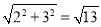 ,BC=4,
,BC=4,
∵AB⊥BD,
∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,
∴△AOB∽△BEC,
∴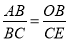 ,
,
即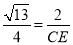 ,
,
解得CE=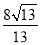 ,
,
∵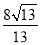 >2,
>2,
∴拋物線的對稱軸l與⊙C相交.(7分)
(3)如圖,過點P作平行于y軸的直線交AC于點Q;
可求出AC的解析式為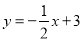
設P點的坐標為(m,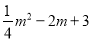 ),
),
則Q點的坐標為(m,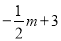 );
);
∴PQ=﹣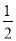 m+3﹣(
m+3﹣(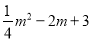 )=﹣
)=﹣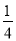 m2+
m2+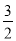 m.
m.
∵S△PAC=S△PAQ+S△PCQ=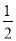 ×(﹣
×(﹣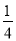 m2+
m2+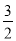 m)×6
m)×6
=-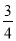 (m﹣3)2+
(m﹣3)2+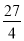 ;
;
∴當m=3時,△PAC的面積最大為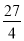 ;
;
此時,P點的坐標為(3,-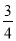 ).
).
考點:二次函數綜合題


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源:2014-2015學年四川省九年級一診數學試卷(解析版) 題型:解答題
學習了統計知識后,班主任王老師叫班長就本班同學的上學方式進行了一次調查統計,圖1和圖2是他通過收集數據后,繪制的兩幅不完整的統計圖,請你根據圖中提供的信息,解答以下問題: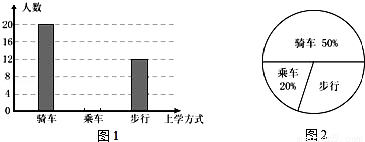
(1)在扇形統計圖中,計算出“步行”部分所對應的圓心角的度數;
(2)求該班共有多少名學生;
(3)在圖1中,將表示“乘車”的部分補充完整.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省九年級一診數學試卷(解析版) 題型:選擇題
二次函數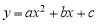 的圖象如圖所示,則下列關系式不正確的是( )
的圖象如圖所示,則下列關系式不正確的是( )
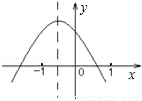
A.a<0 B.abc>0 C.a+b+c>0 D.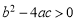
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省九年級一診數學試卷(解析版) 題型:選擇題
為了估計湖中有多少條魚,先從湖中捕捉50條魚做記號,然后放回湖里,經過一段時間,等帶記號的魚完全混于魚群中之后,再捕撈第二次,魚共200條,有10條做了記號,則估計湖里有多少條魚( )
A.400條 B.500條 C.800條 D.1000條
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省日照市莒縣北五校九年級上學期12月聯考數學試卷(解析版) 題型:解答題
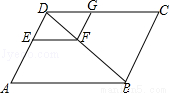
(10分)如圖,在?ABCD中,EF∥AB,FG∥ED,DE∶EA=2∶3,EF=4,求線段CG的長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧省丹東市九年級上學期第二次月考數學試卷(解析版) 題型:選擇題
用配方法解方程x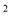 -4x-2=0,變形后為( )
-4x-2=0,變形后為( )
A、(x-2)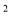 = 6 B、(x-4)
= 6 B、(x-4)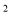 = 6 C、(x-2)
= 6 C、(x-2)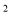 = 2 D、(x+2)
= 2 D、(x+2)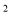 = 6
= 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com