
【題目】如圖,在下列18×7的網格中,橫、縱坐標均為整數的點叫做格點,例如A(﹣8,0)、B(﹣4.3)都是格點.
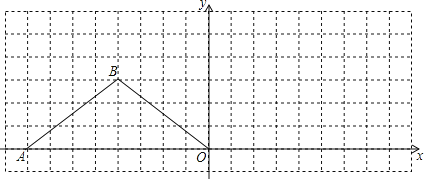
(1)直接寫出△ABO的形狀:
(2)要求在圖中僅用無刻的直尺畫圖:將△ABO繞點O順時針旋轉得△DEO,且點B的對應點E落在x軸正半軸上.
操作如下:
第一步:在x正半軸上找一個格點E,使OE=OB;
第二步:找一個格點F,使∠EOF=∠AOB;
第三步:找一個格點M,作直線AM交直線OF于D,連DE,則△DEO即為所作出的圖形.請你按以上操作完成畫圖.并直接寫出點E,F,M三點的坐標.
科目:初中數學 來源: 題型:
【題目】甲、乙兩人加工同一種零件,甲每天加工的數量是乙每天加工數量的 1.5 倍,兩人各加工 600 個這種零件,甲比乙少用 5 天.
(1)求甲、乙兩人每天各加工多少個這種零件?
(2)已知甲、乙兩人加工這種零件每天的加工費分別是 150 元和 120 元,現有 3000 個這種零件的加工任務,甲單獨加工一段時間后另有安排,剩余任務由乙單獨完成.如果總加工費不超過 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學現有在校學生 1250 人,為了解本校學生的課余活動情況,采取隨機抽樣的方法從閱讀、運動、娛樂、其它四個方面調查了若干名學生,并將調查的結果繪制了 如下兩幅不完整的統計圖,請你根據圖中提供的信息解答下列問題:
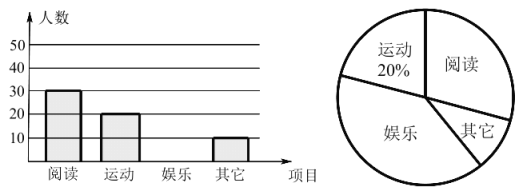
(1)本次調査共取了多少名學生?
(2)通過計算補全條形圖,并求出扇形統計圖中閱讀部分圓心角的度數;
(3)請你估計該中學在課余時間參加閱讀和其他活動的學生一共有多少名
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:今有甲種袋子中裝有黃金9枚(每枚黃金重量相同),乙種袋子中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲種袋子比乙種袋子輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,則可建立方程為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC是⊙O的直徑,弦BD⊥AO于E,連接BC,過點O作OF⊥BC于F,若BD=8cm,AE=2cm,則OF的長度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為邊
為邊![]() 上一動點,設
上一動點,設![]() ,線段
,線段![]() 的垂直平分線分別交邊
的垂直平分線分別交邊![]() 、
、![]() 于點
于點![]() 、
、![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,過
,過![]() 作
作![]() 于點
于點![]() .
.
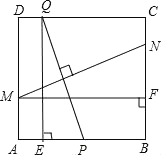
(1)當![]() 時,求證:
時,求證:![]() ;
;
(2)順次連接![]() 、
、![]() 、
、![]() 、
、![]() ,設四邊形
,設四邊形![]() 的面積為
的面積為![]() ,求出
,求出![]() 與自變量
與自變量![]() 之間的函數關系式,并求
之間的函數關系式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D、E分別是AB、BC的中點,F在CA延長線上,∠FDA=∠B,AC=6,AB=8,則四邊形AEDF的周長為( )
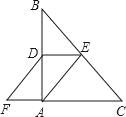
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中數學 來源: 題型:
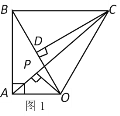
【題目】已知Rt△OAB,∠OAB=90o,∠ABO=30o,斜邊OB=4,將Rt△OAB繞點O順時針旋轉60o,如圖1,連接BC.
(1)ΔOBC的形狀是 ;
(2)如圖1,連接AC,作OP⊥AC,垂足為P,求OP的長度;
(3)如圖2,點M、N同時從點O出發,在△OCB邊上運動,M沿O→C→B路徑勻速運動,N沿O→B→C路徑勻速運動,當兩點相遇時運動停止.已知點M的運動速度為1.5單位/秒,點N的運動速度為1單位/秒.設運動時間為x秒,△OMN的面積為y,求當x為何值時y取得最大值?最大值為多少?(結果可保留根號) .
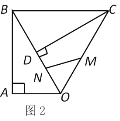

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com