解:(1)若k=0,則y=-2x+

是一次函數,與x軸只有一個交點,滿足條件;
若k≠0,則y=kx
2-2x+

(k≠0)是二次函數,
由△=b
2-4ac=4-6k=0,得k=

.
∴k=0或

.
(2)設反比例函數解析式為:y=

,
∵點M(1,k)在反比例函數圖象上,
∴m=k.
∴y=

.
由反比例函數的性質可知,當y隨x的增大而增大時,須滿足條件:k<0,x≠0.
二次函數y=kx
2-2x+

,拋物線開口向下,其對稱軸為直線x=

,
當y隨x的增大而增大時,須滿足條件:k<0,x<

.
綜上所述,要使該反比例函數和二次函數都是y隨x的增大而增大,須滿足條件:k<0,x<

.
(3)存在.
拋物線解析式為:y=kx
2-2x+

,
令y=0,即kx
2-2x+

=0,
∴x1+x2=

,x1x2=
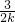
.
∵x
12+x
22=1,
∴(x
1+x
2)
2-2x
1x
2=1,即:(

)
2-2•
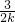
=1
整理得:k
2+3k-4=0,
解得:k=-4或k=1.
又∵拋物線與x軸有兩個交點,
∴△=4-6k>0,解得k<

,
∴k=1不符合題意,舍去,∴k=-4.
∴拋物線的解析式為:y=-4x
2-2x+

=-4(x+

)
2+

.
令y=0,解得x=
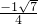
,
∴A(
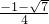
,0),B(
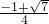
,0).
畫出函數大致圖象如下,則OA=
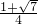
,OB=
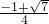
,AB=

.
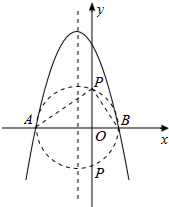
以AB為直徑作圓,由圖象可見,圓與y軸的交點有2個,因此所求的點P有兩個.
連接PA、PB,易證△PAO∽△BPO,
∴
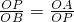
,
∴OP
2=OA•OB=
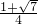
×
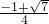
=

,∴OP=

.
S
△ABP=

AB•OP=

×

×

=
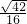
.
綜上所述,存在兩個滿足條件的點P.點P的坐標為(0,

)或(0,-

),△ABP的面積為
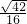
.
分析:(1)本問注意分類討論:若k=0,函數為一次函數;若k≠0,函數為二次函數,根據其△=0求解即可;
(2)根據反比例函數和二次函數的增減性,綜合確定k應滿足的條件和x的取值范圍;
(3)由題意,首先根據一元二次方程根與系數關系,求出k的值;從而得到拋物線的解析式,畫出拋物線的大致圖象,以AB為直徑作圓,圓與y軸的兩個交點即為所求之點P;最后利用相似三角形求出點P的坐標和△ABP的面積.
點評:本題是二次函數綜合題型,考查了二次函數的圖象與性質、反比例函數、一元二次方程、根與系數關系、根的判別式、相似三角形等知識點,有一定的難度.第(1)問中,須分一次函數、二次函數進行討論;第(3)問中,滿足條件的點P有兩個,容易漏解.可見分類討論思想是本題考查重點,也是易失分點.

 (k是常數)
(k是常數) 都是y隨x的增大而增大,求k應滿足的條件以及x的取值范圍;
都是y隨x的增大而增大,求k應滿足的條件以及x的取值范圍; 與x軸交于A(x1,0),B(x2,0)兩點,且x1<x2,x12+x22=1.在y軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由.
與x軸交于A(x1,0),B(x2,0)兩點,且x1<x2,x12+x22=1.在y軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由. 是一次函數,與x軸只有一個交點,滿足條件;
是一次函數,與x軸只有一個交點,滿足條件; (k≠0)是二次函數,
(k≠0)是二次函數, .
. .
. ,
, .
. ,拋物線開口向下,其對稱軸為直線x=
,拋物線開口向下,其對稱軸為直線x= ,
, .
. .
. ,
, =0,
=0, ,x1x2=
,x1x2=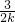 .
. )2-2•
)2-2•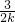 =1
=1 ,
, =-4(x+
=-4(x+ )2+
)2+ .
.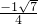 ,
,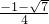 ,0),B(
,0),B(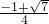 ,0).
,0).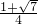 ,OB=
,OB=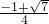 ,AB=
,AB= .
.
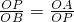 ,
,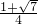 ×
×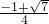 =
= ,∴OP=
,∴OP= .
. AB•OP=
AB•OP= ×
× ×
× =
=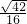 .
. )或(0,-
)或(0,- ),△ABP的面積為
),△ABP的面積為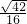 .
.

 全優點練單元計劃系列答案
全優點練單元計劃系列答案 (k是常數)
(k是常數) 都是y隨x的增大而增大,求k應滿足的條件以及x的取值范圍;
都是y隨x的增大而增大,求k應滿足的條件以及x的取值范圍; 與x軸交于A(x1,0),B(x2,0)兩點,且x1<x2,x12+x22=1.在y軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由.
與x軸交于A(x1,0),B(x2,0)兩點,且x1<x2,x12+x22=1.在y軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由.