
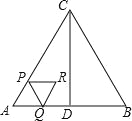
【題目】如圖,△ABC是等邊三角形,AB=4cm,CD⊥AB于點D,動點P從點A出發,沿AC以2cm/s的速度向終點C運動,當點P出發后,過點P作PQ∥BC交折線AD﹣DC于點Q,以PQ為邊作等邊三角形PQR,設四邊形APRQ與△ACD重疊部分圖形的面積為S(cm2),點P運動的時間為t(s).
(1)當點Q在線段AD上時,用含t的代數式表示QR的長;
(2)求點R運動的路程長;
(3)當點Q在線段AD上時,求S與t之間的函數關系式;
(4)直接寫出以點B、Q、R為頂點的三角形是直角三角形時t的值.
【答案】(1)證明見解析(2)2![]() +2(3)①S=S菱形APRQ2
+2(3)①S=S菱形APRQ2![]() t2;②S=﹣
t2;②S=﹣![]() t2+6
t2+6![]() t﹣2
t﹣2![]() (4)t=
(4)t=![]() 或t=
或t=![]()
【解析】
試題分析:(1)易證△APQ是等邊三角形,即可得到QR=PQ=AP=2t;
(2)過點A作AG⊥BC于點G,如圖②,易得點R運動的路程長是AG+CG,只需求出AG、CG就可解決問題;
(3)四邊形APRQ與△ACD重疊部分圖形可能是菱形,也可能是五邊形,故需分情況討論,然后運用割補法就可解決問題;
(4)由于直角頂點不確定,故需分情況討論,只需分∠QRB=90°和∠RQB=90°兩種情況討論,即可解決問題.
試題解析:(1)如圖①,

∵△ABC是等邊三角形,
∴∠ACB=∠B=60°.
∵PQ∥BC,
∴∠APQ=∠ACB=60°,∠AQP=∠B=60°,
∴△APQ是等邊三角形.
∴PQ=AP=2t.
∵△PQR是等邊三角形,
∴QR=PQ=2t;
(2)過點A作AG⊥BC于點G,如圖②,

則點R運動的路程長是AG+CG.
在Rt△AGC中,∠AGC=90°,sin60°=![]() ,cos60°=
,cos60°=![]() ,AC=4,
,AC=4,
∴AG=2![]() ,CG=2.
,CG=2.
∴點R運動的路程長2![]() +2;
+2;
(3)①當0<t≤![]() 時,如圖③,
時,如圖③,

S=S菱形APRQ=2×S正△APQ=2×![]() ×(2t)2=2
×(2t)2=2![]() t2;
t2;
②當![]() <t≤1時,如圖④
<t≤1時,如圖④

PE=PCsin∠PCE=(4﹣2t)×![]() =2﹣t,
=2﹣t,
∴ER=PR﹣PE=2t﹣(2﹣t)=3t﹣2,
∴EF=ERtanR=![]() (3t﹣2)
(3t﹣2)
∴S=S菱形APRQ﹣S△REF
=2![]() t2﹣
t2﹣![]() (3t﹣2)2=﹣
(3t﹣2)2=﹣![]() t2+6
t2+6![]() t﹣2
t﹣2![]() ;
;
(4)t=![]() 或t=
或t=![]()
提示:①當∠QRB=90°時,如圖⑤,

cos∠RQB=![]() ,
,
∴QB=2QR=2QA,
∴AB=3QA=6t=4,
∴t=![]() ;
;
②當∠RQB=90°時,如圖⑥,

同理可得BC=3RC=3PC=3(4﹣2t)=4,
∴t=![]() .
.


 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
【題目】某校欲招聘一名數學教師,學校對甲、乙、丙三位候選人進行了三項能力測試,各項測試成績滿分均為100分,根據結果擇優錄用.三位候選人的各項測試成績如下表所示:
測試項目 | |||
測試成績/分 | |||
甲 | 乙 | 丙 | |
教學能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
組織能力 | 64 | 72 | 84 |
(1)如果根據三項測試的平均成績,誰將被錄用,說明理由;
(2)根據實際需要,學校將教學、科研和組織三項能力測試得分按5∶3∶2的比例確定每人的成績,誰將被錄用,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了豐富學生的第二課堂,對學生參與演講、舞蹈、書法和攝影活動的興趣情況進行調查,學校采取隨機抽樣的方法進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中最感興趣的一項),對調查結果進行統計后,繪制了如下兩個統計圖: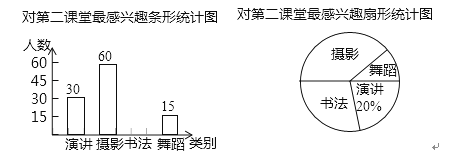
(1)此次調查抽取的學生人數m= 名,其中選擇“書法”的學生占抽樣人數的百分比n= ;
(2)若該校有3000名學生,請根據以上數據估計該校對“書法”最感興趣的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在Rt△ABC中,∠C=90°∠A、∠B、∠C所對的邊分別記作a、b、c.
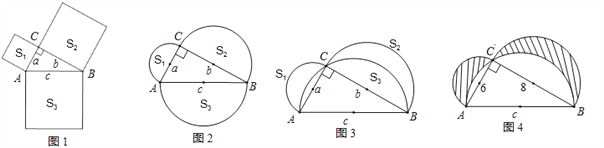
(1)如圖1,分別以△ABC的三條邊為邊長向外作正方形,其正方形的面積由小到大分別記作S1、S2、S3,則有____________;
(2)如圖2,分別以△ABC的三條邊為直徑向外作半圓,其半圓的面積由小到大分別記作S1、S2、S3,請問S1+S2與S3有怎樣的數量關系,并證明你的結論;
(3)分別以直角三角形的三條邊為直徑作半圓,如圖3所示,其面積由小到大分別記作S1、S2、S3,根據(2)中的探索,直接回答S1+S2與S3有怎樣的數量關系;
(4)若Rt△ABC中,AC=6,BC=8,求出圖4中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明解方程![]() 的過程如下.請指出他解答過程中的錯誤,并寫出正確的解答過程.
的過程如下.請指出他解答過程中的錯誤,并寫出正確的解答過程.
解:方程兩邊同乘x,得1-(x-2)=1.……①
去括號,得1-x-2=1.……②
合并同類項,得-x-1=1.……③
移項,得-x=2.……④
解得x=-2.……⑤
∴原方程的解為x=-2.……⑥
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,⊙C過原點O,交x軸于點A(2,0),交y軸于點B(0,![]() ).
).
(1)求圓心C的坐標.
(2)拋物線y=ax2+bx+c過O,A兩點,且頂點在正比例函數y=-![]() 的圖象上,求拋物線的解析式.
的圖象上,求拋物線的解析式.
(3)過圓心C作平行于x軸的直線DE,交⊙C于D,E兩點,試判斷D,E兩點是否在(2)中的拋物線上.
(4)若(2)中的拋物線上存在點P(x0,y0),滿足∠APB為鈍角,求x0的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com